Does a used car need insurance?

StickyOscar

The importance of car insurance cannot be overstated when owning a car, whether purchasing one new or one used. The question of whether a used car needs insurance often arises among buyers. Some people assume since they have already bought the car outright, they do not need insurance. But is this true? A used car needs insurance just like any other vehicle on the road. Even though you may purchase the vehicle with the money and do not owe anything to anyone else, there are still several reasons why need to insure the used car.

Protects you from liability

If someone causes an accident while driving a used car and someone gets hurt while the property gets damaged as a result, they may be held responsible for covering those costs out of pocket if they do not have insurance coverage. The socal mitsubishi for sale has a variety of cars available, ranging from the entry-level Mirage and Lancer to the sporty Evolution and powerful Outlander.

Covers your car against theft or damage

An important reason why auto insurance for a used car is a must is it helps cover damages caused by theft or natural disasters such as floods and hurricanes. Depending on the type of coverage selected, the policy may also pay for repairs if the vehicle sustains damage in an accident. Insuring a used car provides peace of mind that you are protected in case something unexpected happens while driving.

Do you need a certain amount of insurance?

The amount of insurance required for the used car will depend on several variables, including the age and value of the vehicle, your driving record, and your budget. Essential to carry enough coverage to protect yourself from financial loss in case of an accident or incident results in damages or injury.

Liability coverage

Most require drivers to carry a minimum amount of liability coverage. Liability insurance covers other parties involved in an accident with you when you are at fault. This type of coverage does not pay for damages to your vehicle but may cover injuries, medical bills, or property damage caused by you. Comprehensive auto insurance provides coverage against theft, vandalism, natural disasters such as floods and hurricanes, fire, and other non-collision events. It may also cover windshield repairs or replacement and animal collisions. If you need more information, visit this web-site.

Collision coverage

Collision auto insurance pays for damages to your car if it collides with another vehicle or object. This is regardless of who is at fault. It is also possible for lenders to require collision coverage until loans are paid off accordingly on their policies. One such responsibility is having adequate auto insurance coverage to protect yourself from accidents, liability claims, and unexpected hazards on the road. You should fully understand what types of coverage are available and how much you can afford before purchasing insurance. This will ensure you are covered no matter what happens behind the wheel.

How to Determine the True Value of a Used Car

StickyOscar

When shopping for a used car, one must assess its true worth before making a purchase. Assessing a used car’s true value can be challenging due to factors like condition, mileage, age, and market demand; however, you can take certain steps to determine this figure accurately. In this article, we’ll look at some of the most reliable methods.

Research the Market Value

Research its market value to determine the true worth of used cars in phoenix. Various online tools can assist with this research; websites like Kelley Blue Book or Edmunds offer estimated values based on age, mileage, and condition. You may also check online car listings to see what similar vehicles are selling for in your area.

Consider the car’s condition.

When purchasing a used car, the condition is one of the most critical factors in determining its true worth. Before making an offer on any car, be sure to inspect it thoroughly, both inside and out, for signs of wear and tear, such as dents, scratches, and rust. Inspect all components, such as tires, brakes, and suspensions, to ensure they work well. You may even want a professional mechanic to inspect the car to identify any potential issues.

Evaluate the car’s mileage.

Mileage is another factor to take into account when assessing a car’s true worth. Generally, lower mileage translates to greater value; however, this can vary based on the make and model. For instance, high-performance sports cars may have greater intrinsic worth with higher miles due to their designed capacity for hard driving.

used cars in phoenix

Check the vehicle’s history report.

Before purchasing a used car, it’s essential to check its history report. This will give you crucial details about the car’s past, including any accidents or major repairs. A vehicle history report can be acquired through services, providing you with valuable insights into its past.

Consider the demand for the car.

Finally, when considering which car to purchase, demand should be taken into account. If a car is popular and in high demand, its value may increase due to factors like popularity, availability, and unique features. On the other hand, if demand for your desired model isn’t high enough, its value could decrease.

In conclusion, accurately determining a used car’s true worth requires considering several factors. Researching market values, inspecting condition and mileage, checking its history report, and considering demand can give you an accurate sense of its worth. Investing time to do your due diligence and make an informed decision will enable you to find a dependable, high-quality used vehicle that meets your needs and budget.

What Are The Advantages Of Wearing A Tennis Bracelet With Diamonds?

StickyOscar

Tennis bracelets with diamonds are classy, classic pieces of jewellery that have been in style for many years. They go with every outfit and are adaptable. Tennis bracelets made of diamonds provide an advantage over being fashionable. To sum up, the diamond tennis bracelet is more than just a beautiful piece of jewellery.

Brightens up any outfit

A diamond tennis bracelet has the brilliance that is characteristic of diamonds. It can give every ensemble a dash of glitz and refinement. Also, the diamonds’ brilliance can highlight your wrist and give your outfit a touch of class.

Versatile

Tennis bracelets made of diamonds are stylish and go with every attire. They can be dressed up for a formal occasion or down for a more laid-back style by pairing them with jeans and a t-shirt. They are a terrific investment because of their timeless design, which makes them suitable for any situation.

Classic and Eternal

Tennis bracelets with diamonds have been around for a while and are still a common jewellery item. Because their timeless design ensures that they will never go out of style, they are a fantastic investment. A diamond tennis bracelet can utilise the generations while maintaining its magnificent appearance.

Enhances Other Jewellery

Tennis bracelets with diamonds are a terrific addition to any jewellery collection because they go well with other pieces. They go well with diamond rings, pendant necklaces, and diamond stud earrings. The bracelet will not compete with other jewellery pieces because of its timeless style.

Love and affection symbol

A diamond tennis bracelet can represent affection and love. It can be presented as a gift to a loved one to express how much you value them, such as a spouse, mother, or daughter. A diamond tennis bracelet can help as an enduring memento of affection. And love two individuals have for one another.

Money-Making Piece

A diamond tennis bracelet might be an investment because diamonds are a precious commodity. It’s crucial to pick a bracelet with diamonds verified by an accredited laboratory. A certified diamond increases its worth by ensuring it is of the highest calibre.

Encourages Confidence

Tennis bracelets made of diamonds can increase your self-esteem and make you feel pretty. The traditional design may lend a touch of refinement to your entire appearance, and the brilliance of the diamonds can assist attention to your wrist. You may feel proud and self-assured knowing that you are sporting a piece of fine jewellery.

Preowned cars are better to be purchased than the brand new cars

StickyOscar

Internet lending platforms have made it easier for you to get financing by eliminating the barriers you face when working with traditional lenders or banks to purchase used cars in el cajon. They also give you a chance to get a loan for a used car. The interest rate on a loan for a used car will indeed be higher than the interest rate for a new car.

Still, it’s also true that the interest rate on loan for a new vehicle will be lower than the interest rate for a used car. After completing the application’s registration process, your eligibility will be checked. The credit line will be approved and sent to you within a few minutes.

The buyer makes a big commitment when they spend a lot of money on a car

Do your homework, just like you would for any other investment you might want to make. Consider all the factors contributing to taking the decision of used a car purchase. People who have never bought a vehicle often make the mistake of buying a car that doesn’t meet their needs or leaves them with too much debt to handle.

Your first step should be to look into what made you buy a used car. It’s possible that your family’s living situation has changed, the maintenance cost has gotten too high, or it’s just time for a change. Even though there is no clear answer to this question, it is a significant step that will help you with the rest of the steps you need to take to buy a car.

Now is the time to figure out what made you decide to buy a car in the first place. For most people, this could be about a way to get around, a helpful thing, or even something fun. If you know exactly what you want, you can rule out some options, like fuel-efficient hybrid cars, powerful pickup trucks, and sporty coupes and convertibles. You might also want to get a car with many uses, like an (SUV).

Why are the Instagram Users Purchasing the Views from Engagement Platforms?

StickyOscar

People are always interested in communication between them and if that will be very easy then that is always good for them if any tools are used for that then immediately they will access it. Here we are not going to see about the tools but need to look out for the platforms. Technology development and the internet availability made the way to create more technology-related products and also the facility that can be used by the people. In this concern, if we look at the platform that can be used online then we could not avoid the social media platforms such as Facebook, Instagram, and Twitter. Most people use this for communication with each other and also to express their thoughts.

Usually, on social media, people will share photos, videos, and also their daily activities on their page in social media platforms. Those platforms, Facebook and Twitter have been used from the early stage of social media whereas Instagram is developed later and this can be mentioned as a simple form of one of the social media called Facebook. Here, on Instagram also people can post their content in various forms. Sharing photos and videos on social media will have a lot of benefits. Actually where the people are more that place will be an active one for the marketing of all the products. On this social media is also having more population hence social media or Internet marketing will be intensively working and start to promote the products to increase sales. For this promotion, the companies and brands will be used the active users and will pay them a decent amount.

On what basis they will pick and use them? Actually, the active users will always have more followers and also their posts will get more views and likes. These details directly inform that they connect with more people through the Instagram platform. So if the company uses its page to promote the products then there are chances of increasing sales. But, not all users will get more followers as well as may not get more views for their posts. In fact, it is more difficult to reach decent followers and view them organically. Hence the users will use various strategies to reach the maximum numbers in a quick time. Purchasing Instagram views is one of the strategies that will benefit them to reach the expected numbers. There are many engagement platforms that offer this with different packages like 1000 and 5000 views Instagram hence the users can pick anyone for their benefit. Though it is not ethically good, from a business perspective many are doing it and they have to purchase these from reliable sites for a better outcome.

Take Attention To Blood In Stool!

StickyOscar

Maintaining a healthier lifestyle is very important. A simple modification in our lifestyle can lead to a better life. For example, drinking 3 to 4 liters of water per day will cure many diseases. We don’t have time to care for health in this modern society. Untaken care of health has resulted in an unhealthy lifestyle. Nowadays, one of the main problems faced is blood in stools.

Causes for Blood in stool:

Blood stool can be a symptom of a severe problem in your digestive tract, ulcer, or inflammation. Blood in stool doesn’t mean it should be red; it may also appear black and tarry. Several health issues can lead to blood in stools. For example,

Colon polyps: a person having colon polyps will mostly not have any symptoms, but he can notice black stool. He will be suffering from fatigue. There is no specific reason for the appearance of polyps, but as you grow older, it causes polyps.
Inflammatory bowel disease: this disease includes ulcerative colitis and Crohn’s disease. The symptoms of this disease are weight loss, fatigue, abdominal pain and diarrhea.
Peptic ulcer: peptic ulcers are caused in the lining of the stomach and cause Blood in stool. The symptoms are nausea, vomiting and weight loss.

Blood in stool is the symptom of many other diseases like diverticula, haemorrhoids, anal fistula, the digestive tract, medication and cancer. Blood stool in children may be due to superficial reasons, such as structural changes, food allergies, etc.

Every problem has a solution:

In this advanced world, we have solutions for every medical problem. Wright, from heart operations to simple cases, every disease has a solution. When you visit a physician for a blood problem in stool, he will ask you how much Blood is visible?, whether you are having any pain?, and how often Blood appears.

In case of an emergency, the doctor will perform an endoscopy. In non-emergency situations, the doctor will perform a fecal immunochemical blood test( FIT), complete blood count, digital rectal examination or endoscopy and provide you with proper treatment. In some extreme cases, surgery is also possible.

Cure in earlier stage:

One should seek medical attention as soon as he notices the symptoms of back and dark red Blood in stool, unexplained stomach pain, diarrhea, weight loss, nausea, and pain when passing stool. Visit a physician in the earlier stage for proper attention.

Overall, don’t hesitate to visit a physician. When you see a symptom, call a doctor to cure it as soon as possible. To know more information, visit the website https://curasia.com/blood-in-stools-colorectal-cancer/.

Advantages Of Buying Used Cars In Sacramento

StickyOscar

It is more financially advantageous to get a used car that feels more comfortable than a new car in Sacramento. The advantages of purchasing used cars go far beyond the financial savings. Among the advantages of purchasing used cars in sacramento are:

Inexpensive price

Older cars are always far less expensive than newer models, but inheriting their flaws is never ideal. By confirming that the car is recognized, one can decline with ease. If they’ve always wanted a luxury vehicle but are unable to afford one owing to financial constraints, purchasing a used model enables an individual to easily experience the delight of driving a vehicle. luxurious vehicle

Low rate of depreciation

The preferred depreciation rate for vehicles is higher for new vehicles than for older vehicles. The car’s value decreases by one mile per month. However, the largest impairment, which was close to 40%, happened in the first year. Individuals won’t experience this depreciation if they purchase a secondhand vehicle. There is also less mental depression because they aren’t concerned about damages and leftover paint in the parking lot.

Cheap premium

The life of the car has an impact on insurance rates the same way that loans do. However, insurance costs are typically lower for secondhand cars. Regardless of the vehicle buyer decide on, anyone who is willing to do some homework before making a purchase can avoid insurance charges.

Guarantee

One can also be qualified for a car warranty if one purchases a used automobile through a company-owned utilized car dealership. However, this guarantee has some restrictions and is only valid for a particular number of miles driven during a specific time frame.

Tax on spending

The majority of auto advertising typically discusses taxes. Many state rules charge taxes on brand-new car purchases but not on old ones. Used automobile buyers could save a significant amount of cash in this way.

Wrap-Up

The days of secondhand automobiles in Sacramento being associated with worn-out exteriors, inside, and injuries are long gone. Customers of today can restore a used car to like-new condition while maintaining its dependability. One has options when it comes to used cars, and the individual may pick one that is mechanically sound and free of dents. Purchasing used automobiles in Sacramento from reputable dealers has several advantages. With a used model, one can have the same level of comfort and usefulness for less money. It’s preferable to buy a new one.

Growing Business Of Honda Fresno And Other Cities

StickyOscar

The growing car rental services not only in India but nations world-wide have outshined the new car sales, which has dipped immensely over the past few years. The pre-owned car market has grown by leaps and bounds with more and more people buying a second hand, fully functioning certified cars rather than replacing their old vehicle for a brand new one. It is a much cheaper and affordable option for all those unwilling to spend extra bucks on buying a recent model.

Growing preference:

Not only in India, but the growing demands of second-hand cars all across the world have made this industry a major hit. The honda fresno are a much more preferred and popular option amongst the interested. So why do people are having this shift in preference? Recent reports state that people find used cars as a good value for their money, which is nowhere a point of surprise with our increasing disposal income and the economic development we have.

Since the value of the car significantly depreciates in its first year itself, therefore the buyer’s aspiration of owning a car, at a much lower rate is fulfilled, making used cars a better choice. According to the survey conducted by the companies of honda fresno, amongst four people who replace their old car with another one, only one actually buys a new model while the rest three settle for a pre-owned car.

Reasons for the shift in perception:

According to the experts, the industry of pre-owned cars is driven not by demand but by supply majorly. The average ownership period for a car in most of the cities have come down to three to five years as compared to eight to ten years in the past. Due to this change in law, a car as good as new is also given up for sale after three to five years of use. Some more reasons to go for second-hand cars are:

A well functioning car can be bought at half its original price.
It is smarter as well as a cheaper option.
With growing online marketplaces for pre-owned cars, it has become much more accessible and thus preferable.
It is affordable and values for money.

While buying a new model is always fun but for all those who are on a budget and also want a better, upgraded model of cars, used car services are the best available choice.

Are you interested to learn more about treatment options for pigmentation?

StickyOscar

The customized treatment plan is considered to be very useful if you want to deal with pigmentation disorders. You can ensure to get rid of the presentation problems with the best services offered by our team. The live chat service is always available on our website to resolve the queries of the customers about Pigmentation removal using laser. Careful inspection will play a key role to focus on the color and distribution of the skin. The success of the pigmentation removal treatment can be identified when they get in touch with the experts.

The laser treatment is always conducted in a few sessions to deal with the pigmentation.
There will be no obligations for the individuals if they want to make use of pigmentation removal services.
The medical assessment will be done at the right time so you can treat the condition without any issues.
If you want to learn more about the aesthetic services then you can visit our website.
The oral medications should be followed carefully if you are worried about the customized treatment.

Focus on prolonged treat

The best guidance is offered by the experts to offer protection and care for your skin. An accurate diagnosis is always required to understand the different modalities of the treatment. The importance of sun protection should be taken into consideration to understand the success of pigmentation. The prolonged treatment durations are always required if you want to complete a few sessions related to Pigmentation removal using laser. You can try to get rid of the pigmentation disorders with the recommendations offered by the experts. It is not an easy task for individuals to find the best treatment option according to their requirements.

Get the complete medical advice:

The protection is provided for your skin so you can ensure to complete your treatment in a few sessions. Complete medical advice is provided so there will be no issues for the patients. The terms and conditions should be verified by the individuals if they want to make use of the treatment options. The oral medications will be handled with care so there will be benefits for the patients with the treatment plans. The price list should be taken into account by the individuals when they get access to treatment options. Prolonged treatment durations are required if the treatment process cannot be completed in a few sessions.

A letter requesting an emotional support animal provides many benefits.

StickyOscar

The central motivation behind everyday reassurance creatures is to supply with friendship, ease sadness, and work in battling misery, tension, and explicit silly feelings of trepidation. An Emotional Support Animal Letter is myesadoctor.com a solution or proposal by the Licensed Mental Health Professional that affirms the psychological or profound inability and states that the species is getting valuable benefits from an Emotional Support Animal. We should learn some advantages of having an Emotional Support Animal Letter.

If you want to go for a get-away and need to take your pet along, an ESA Letter is the legitimate consent to take it alongside you on the flight. Various regulations let you travel with your Emotional Support Animal, and anmyesadoctor.com ESA Letter will give you a pal to go along. With a substantial ESA Letter, you can fly with your ESA. An Emotional Support Animal Letter is a kind of permit that works with you in taking your ESA where you can’t take typical pets.

A substantial ESA Letter excludes you from paying the expenses you need to pay for keeping a pet with you. ESA Letter forgoes the pet arrangement on your ESA. Likewise, you are permitted to visit a spot without any pet charges. Once in a while, individuals will not keep a pet at their place because of their age. According to the Emotional Support Animal Laws, Anyone should not Emotional Support an animal regardless of age, weight, size, or breed. You can Keep any pet as ESA that is assisting you in working on your wellbeing with molding.

ESAs are the most dependable companions with a significant amount to propose to the proprietor. An ESA is a trustworthy companion that will help you during difficult situations and blesses you with close-to-home consideration, love, and friendship. It empowers you to manage pressure, uneasiness, and any psychological maladjustment by humoring you in a wide range of exercises. In any case, you really want a substantial ESA Letter to get such a dear companion.

There are many pet confined regions where the pets can’t move out. Nonetheless, this doesn’t matter to the ESAs. Everybody knows about the COVID-19 impacts that everybody is experiencing, affecting people and creatures. During the severe lockdown, different pets were not permitted to move out. With an ESA Letter, ESA proprietors can go out with their ESA, so the patient’s psychological state doesn’t decline.

A Guide to make Perfect Popcorn

StickyOscar

This is a quick and easy way to make popcorn at home if you can’t get to a movie theater or want the experience at home.

A very crisp popcorn: Popcorn cooked in ghee won’t turn soggy or stale-tasting because it’s not moist.
Cinema-quality popcorn! It may shock you to learn that you can make popcorn at home, especially if you love that big tub of traditional salted popcorn. Several unique ingredients work together to achieve this.
Get started now! You’ll enjoy a popcorn bowl in less than 10 minutes after gathering all your ingredients.

This recipe requires the following ingredients.

Coconut Oil – Yummy movie theater traditional salted popcorn contains coconut oil – they pop the kernels in it! Its high smoking point makes it perfect for popping popcorn and delivering that unique flavor. As a substitute, you can use canola oil, vegetable oil, or peanut oil.
Popcorn Salt – A specialty ingredient known as popcorn salt is superfine, so it can easily be incorporated into each kernel. Put your kosher salt in the food processor to make it ultra-fine, then label it “popcorn salt” and store it.
Popcorn Kernels – There is a wide selection of popcorn kernels here – yellow, white, and Amish; choose your favorite!
Ghee – Butter that has been clarified by removing any water or milk solids is why the popcorn doesn’t get soggy. Ghee is available in most stores worldwide now, but you can also make clarified butter at home!

Clarified butter recipe:

Simple and quick to complete, the process takes no time at all. Follow these steps:
One pound of butter should be simmered over low heat for about an hour.
Skim any excessive foam off the top and discard.
Line a medium bowl with a fine-mesh sieve.
Lay two layers of paper towels or cheesecloth in the sieve.
Place the sieve over a bowl and pour the remaining melted butter through.
Refrigerate for up to three months after cooling to room temperature.

Popcorn made on the stovetop

Over medium heat, melt the coconut oil in a large, heavy pot.
After 30 seconds, remove the pot from the heat. Add three popcorn kernels after the oil has melted. Stir in the salt and remaining popcorn kernels once those three kernels pop.
Continue cooking popcorn on medium heat. When popping the popcorn, ajar the lid slightly so that steam can escape and shake the pot occasionally.
Once the popcorn has popped for two or three seconds between pops, please remove it from the heat and put it into a large bowl to serve.
Then, add the melted ghee to the hot pot (no need to turn it back on). Toss the popcorn with the melted ghee and serve.
Enjoy: Taste and adjust the taste if necessary, then add more salt or clarified butter.

Which are the best cakes in Singapore?

StickyOscar

The Bakery Boy is a specialized bakery that creates the best cakes in Singapore for any event, including weddings and birthdays. There are many different types of celebrations, including birthdays, weddings, anniversaries, and longevity celebrations. Cakes with a Reduced Sugar Content

Chiffon cake layers are tender and delicious, and here are cakes made to order that are lower in sugar content than conventional cakes. These are all Uniquely Designed.

Cakes with one-of-a-kind designs and extensive personalization that are handcrafted to order for all of your special occasions. When the total value of your order is $150 or more, shipping is free of charge (3-hour range delivery, 9-6 pm).

They do not use pig or fat in their products and have Muslim staff, yet we have not yet been given our Halal certification despite the fact that they utilize it.

In most cases, they do not include alcohol in any of our cakes; however, if the cake requires a gold painting or an alcohol bottle as decoration, they may make an exception (they will throw the alcohol in the bottle away). If the establishment at which you are placing your order requires the cakes to have halal certification, all they can do is present you with a list of the ingredients that are used in the preparation of the cakes.

Every cake delivery will come with a gold-colored candle that is extra long and a birthday knife that can only be used once.

In order to eliminate any possibility of salmonella contamination, each egg that went into the preparation of our cakes was properly cooked.

Delivery options

The best cakes in Singapore are delivered to you with ease. If your order total is less than $150, you have a few options to choose from, including the following:

The cost of flexible delivery is $9.90. (They will come anytime between 9-630pm)

Delivery on a Regular Schedule – $15.00 (They will come between your preferred 3-hour range between 9-6 pm)

A flat fee of $35 for early delivery between 8 and 10 a.m.

Personalized delivery timing within a range of one hour costs $35. (Latest 5-6 pm)

If your delivery address is to a hotel, chalet, or office building, they will send your package to the nearest car pick-up and drop-off spot, and our delivery person will phone you prior to delivering your package.

If you would like the cake to be left at a restaurant for you, please let us know the name of the table that you have reserved it under. This will allow us to label the cake with your name.

Are you willing to play a free game in your free time?

StickyOscar

Are you a fan of online games? Are you worried about the cost of the game? Don’t bother about the cost, for you there are many free games which will help you a lot. All over the world is now controlled only by the online, because from children to old people are all like to surf in internet and love to play the games. Now, all have smartphones, but some have it for other purposes such as calling, chatting, etc. But many of them use it for playing 먹튀검증 games, and a few years ago, this sort of video game was only played and enjoyed by children, but nowadays, everyone likes to play this game. You can watch those people who use smartphones anytime, but they only play games.

How to find the latest games?

If you are searching for the latest, most awesome and different games for free, then there are many websites available for you. There you can find a whole host of fantastic puzzle games, action-based games, hidden object games, and so on. Do you like to play car race games or perhaps hidden object games, and then there are more games available in that you can prefer any games which you like most and it is easy and quick to download. For increased internet safety, always go through an official website only for free games, which prevent you from hackers.

In addition to games, you can also download other things that can be useful to you. Also, you can play directly online, which has many features and is much easier to access. As a coin has two sides like that these also have pros and cons. You don’t have to drive your car to the store to play your favorite games by sitting in a comfortable place, you can download it, and you can enjoy your game.

Is a sports game safe for playing?

Playing sports games might increase your decision-making skills and cognitive ability. Huge numbers of sports games are there, but it is always advisable to choose the best one according to your requirements. The online team-up component is one of the most attractive features of sports games. This kind of the game offers an amazing 먹튀검증 sports experience because it is a replica of the original game. Whenever you feel stressed, then you can play sports games because it is the best way to get rid of from stress

Make your Easy Fudgy Brownies with this recipe.

StickyOscar

This is my outright most loved brownie recipe. They are rich, fudgy in the center, and made totally without preparation. These brownies are much better than the container, and I bet you have what you want to make them previously sitting in your kitchen. Leap to the Easy Fudgy Brownies Recipe

I know that colloquialism these are the “best brownies of all time” is an intense assertion. However, we trust it. I love brownies that are rich and extra chocolaty. These brownies with thick, fudgy middles and creased beat convey! These are ideally suited for boxed brownie sweethearts. The wide, wet, and fudgy surface aren’t the same as what you can anticipate from the boxed blends. However, it improves. These brownies are considerably more delightful than anything produced using a crate. They taste astonishing.

Brownie Ingredients

There’s also a decent opportunity you have the fixings available. Allow me to walk you through the means for making them. If you love essential recipes like this one, investigate these blondies, or cacao powder brownies treats. Both are astounding! These brownies require one bowl and meet up in minutes. You’ll need this:

Spread adds a great deal more flavor than oil at any point could. We utilize 100 percent spread in the recipe and don’t want to add oil.

Sugar adjusts the sharpness of unsweetened cocoa powder and adds to the surface of the brownies. It makes the focus delicate and the tops crimped.

Cocoa powder adds our chocolate component and makes these taste rich. I’ve utilized an assortment of cocoa powders. You can use regular cocoa powder, Dutch-handled cocoa powder, or crude cacao powder to make these. Use what you love; however, I love the kind of Droste Cacao, a Dutch cacao powder brownies. Eggs add wealth and give design to the brownies.

Salt and vanilla assist in balancing the kind of the brownies. Salt in baking could appear odd, yet very much like in exquisite cooking, it stirs the types of the recipe. All-reason flour is the last fixing you want, yet you don’t require much. Remember that we’re on the chase after extra fudgy brownies and downplaying the flour assists. Cakey brownie recipes will call for more flour. While we have not attempted this ourselves, assuming that you read through the remarks beneath, many individuals have had achievements utilizing a sans gluten flour mix (like the Bob’s Red Mill mix).

Pontoon boat accessories that you must have for family fun

StickyOscar

Pontoons are one of the most adaptable boat forms due to the sheer variety of activities that can be done onboard them. With the addition of a couple of accessories, your pontoon can accommodate almost any demand, from fishing to water sports and so much more. There are numerous pontoon boat accessories available, and choosing the proper ones for your boat can be tricky, so we have compiled a list of few favourites for you. It is better to learn about electric trolling motor for pontoon boat

TurboSwing ski tow bar

Start pulling tubes to boost the fun factor on your boat and there is no better or safer way to do so than with a TurboSwing ski tow bar. TurboSwing’s innovative design attaches to your boat’s transom (the strongest point of your boat) and is the only tube-rated towing equipment on the market. The fun doesn’t stop there. Installing a TurboSwing gives an elevated tow point that works well for wakeboarding, kneeboarding, water skiing, and other activities.

Heavy-Duty tow rope

To pull your towable tubes behind your TurboSwing, you will need a correctly sized tow line. Tow ropes used for tubing must be at least 50 feet long and no longer than 65 feet, according to the Water Sports Industry Association (WSIA). It is also vital to think about how many riders you will be pulling. The higher the tensile strength of your rope, the more weight you should be pulling.

Waterproof portable Bluetooth speakers

Any day on the water is better with your favourite music playing in the background. If you don’t have speakers installed on your yacht, a portable speaker is an excellent substitute. When it comes to choosing the appropriate portable speaker, opt for one that connects to your phone via Bluetooth and is waterproof so it stays safe while on the water. Try learning about electric trolling motor for pontoon boat

Water slide

Whether you install a water slide as a permanent fixture on your boat or choose for an inflatable slide that you can take down and set up as needed, a water slide adds a whole new level of fun to your pontoon boat. You and your family will enjoy sliding off the deck of your boat time and time again.

Pontoon grill

After a day on the lake, there is no better way to keep the fun and relaxation going than by grilling up a fantastic lunch. The open shape of a pontoon boat’s deck makes it ideal for cooking up your favourite cuisine. Keep in mind, however, that you should only grill when the boat is stationary.

Weatherproof pontoon boat cover

Every boat needs a cover, but which cover is best for your pontoon boat? We highly recommend searching for a good company for all of your boat cover needs. Shop by boat model for an Exact Fit cover that is perfectly patterned to your boat, or shop by boat style for a Select Fit cover that’s patterned for your boat’s overall shape and sized in one-foot increments for the closest possible fit.

Reasons to Go Hiking That Convince You Get Outside

StickyOscar

Are you bored with the same routine workout? Need to admire adventure and get connected to nature? A perfect hike will make you do so. To start hiking you do not need any specific skills, it is just like putting one foot in front and of the other. Even if you have difficulty sleeping on certain nights, consider including hikes or even outdoor walks in your training program. Other than curing the sleeping disorder, adopting a new fitness challenge, and getting some fresh air to breathe, there are some healthy payoffs of heading for hiking in Colorado.

It could help you lose weight

Any type of exercise can help you lose weight as long as you burn more calories per day than you ingest. In contrast, hiking may help you lose weight quicker than other types of exercise since you can burn more calories in less time. Hiking outperforms milder exercises like walking, yoga, and tai chi when it comes to weight reduction simply because it is more strenuous.

Hiking helps to strengthen your lungs

Cardiovascular activity of any kind might help to strengthen your lungs and your entire cardiorespiratory system, which includes your heart, lungs, airways, and blood vessels. Aerobic activity such as walking, hiking, jogging, swimming, dancing, stair-climbing, and even interval training enhances lung capacity. What distinguishes hiking in Colorado from walking or running on flat ground is that the uneven terrain, switchbacks, and inclines will push your cardio-respiratory system in ways that walking or running on level surfaces would not.

Hiking can aid with blood sugar management

Hiking on a regular basis may help you avoid or manage type 2 diabetes by reducing your blood sugar levels. Hiking works your muscles, requiring your body to transport glucose from your bloodstream to your working muscles for energy.

A series of treks over time can make a significant effect on your normal blood sugar levels. Aerobic exercise, or any type of steady-state activity that activates the main muscles and increases heart rate and breathing rate, maybe highly good for diabetics. An eight-week aerobic exercise program can increase insulin sensitivity, body weight, and waist circumference in persons with type 2 diabetes.

Keep in mind that you are at the hands of changing weather and, at times, unforeseen terrain. Always trek with a companion or, at the very least, notify friends and relatives back home of your location before setting out.

What is the need for an eat-and-run verification site and its services?

StickyOscar

Because of the present dynamic lifestyle and technology-advanced market, there are a lot of challenges in choosing quality products and finding the best availability. In a lot of cases, people come across inappropriate products and websites, finally getting cheated or scammed. Presently, we need to understand; along with good quality standard products and authentic websites, many fraud and scam websites also run through the market and try to fool clients. But, you must not get into the trap. 먹튀검증사이트(eat and run verification) can be your lifesaver in this case.

Points to remember in case of choosing any website

Before choosing, you must check the authenticity of the website. All websites need to have proper legal documents to prove that, they are genuine. Therefore before investing in any website, you must check whether they have a legal license and secured transaction process.
You must be aware of the product specifications and its quality standards. You must, always check out the entire control criteria of the product, such as storage, dates, delivery, availability, supply, etc.
Check whether the website is on the scams list or not. You can get good information about this by reading reviews. Always check the previous reviews given by the clients so that you can get the real-market picture of what the website offers, is it worth investing in or not.

In today’s organized industries, there are a lot of different aspects of growth within the sectors. 먹튀검증사이트 will offer you avoid the range of products from different brands and retail outlets. Because of this huge availability, somewhere the risk of getting scammed also lies in the market. Therefore to be on the safer side, you must follow the above-mentioned points to prevent yourself from getting into a trap and get the best.

How and where to play online Harry Potter House Quiz

StickyOscar

If you are among those people who love Harry Potter, then you must have a question in your mind like in which harry potter house you would have entered. So, if you want to know the answer to this question, then there are a lot of platforms available online which allow you to play different kinds of quizzes to know the name of the house in which you would have entered. Now every platform has different features and they analyze different factors to put you into our house, so there will be chances that you might enter a house in which you don’t want to. In addition to it, you will find a lot of platforms available online to play, but all of them will not be very interesting. There are many platforms which may sound very boring to you and it may not be easily interesting. So, it becomes very important to choose a platform that is interesting and fun to play and know the answer as well at the same time.

Well, if you are a Harry Potter fan, then you must know the four houses and you must know what all four houses depict in terms of the personalities of the people. So there are chances that you might have one or maybe two houses on your mind in which you want to enter, but there will be chances that you might end up entering another house. In such cases, you would definitely like to take a retake, so you need to choose a platform that allows you to play it again. Well, one of the platforms that you can certainly refer to play Hogwarts house quiz or Harry Potter house quiz is Quiz Lagoon. Over here it is quite easy to play the game as you just have to click on start. Well now let’s see some of the features of this particular website.

Features of Quiz Lagoon

One of the interesting features that this particular platform provides to the users is that it allows you to retake the quiz. Well, if in the first go, you end up entering a house which is not good for you, then you can retake the quiz and there are chances that you might end up inin another house which you would have liked. Apart from this, once you start playing the quiz, you would see different visuals related to Harry Potter and there will be a total of 30 questions that will be asked for you and you would have to answer each one by one. All these questions are related to Harry Potter itself but they are really being asked to change your personality and determine the house in which you would enter.

How Chauffeur service is helpful for business trips

StickyOscar

Chauffeured services are a must for business travelers, and anyone who travels a great deal for work can tell you how important it is to select the best car services. Similarly, if you run a business that hosts clients regularly from out of town, you may also hire a car service to take them to their destination.

No matter if you are the traveler or the host, there are a few things that you can keep in mind to ensure that your trip runs smoothly. You can expect the same thing from your chauffeur services, since they are often based on mutual courtesy and professionalism.

It is important to look at things like how the vehicles are maintained and how the drivers conduct themselves if you want to figure out whether the car service is right for you.

Inquire about the clients the company has served in the past to gain an understanding of the quality of security chauffeurs services it provides. If you are a business traveler, make sure to find a company with experience in planning such trips.

Size should also be considered. Small businesses will have a difficult time keeping up with client demands and dealing with air travel, which is sometimes unpredictable.

We can all agree that flight plans can change without much notice, and a car company with a respectable size will have the staff and flexibility to deal with that.

Size is also affected by location. That also ensures the safety. When it comes to having the ability to navigate around a city, you would know what to expect if you have ever traveled to a place where you used the services of a chauffeur company.

In many industries, adaptability is critical, and the travel industry is no different. If you have a variety of vehicles for different occasions, you can deal with unforeseen circumstances, and your needs will be met.

Depending on your travel needs, you may require different types of vehicles. For instance, a minibus might be necessary. The chauffeur service should be able to provide one.

People may travel in the name of their business for a variety of reasons, and a car rental company that is interested in booking your business should be able to accommodate you or your clients for whatever reason they may be traveling. They could not spend time to check their route is safe or not. This could be found by the Chauffeur services.

If you read this, you will be able to select the most appropriate security chauffeurs service no matter where you travel or where you host travelers. Knowing what to expect and what to look for will help you handle ground travel arrangements quickly, so you can focus on the more important aspects of the safety trip.

Everything You Need To Know About Blood Sugar Level And Its Management

StickyOscar

Blood sugar levels can be effectively managed and adjusted if there is a slight change; either it gets higher or lower. Such actions are to be applied carefully for a healthy you. This article talks about how a person can manage the blood sugar level in his body with the assistance of a diabetic blood sugar levels chart and provides guidelines that are suggested to be followed by you. Let’s dive right in.

Management of blood sugar levels in your body

You can either raise the level of blood sugar when it gets low or lowers it when the level of blood sugar gets high.

In case of a low level of blood sugar

A person suffering from hypoglycemia or a very low level of blood sugar might notice symptoms such as:

Feeling jittery or shaky
Feeling lightheaded or dizzy
Being confused
Having headaches
Being tired or hungry easily
Witnessing changes in heart rhythm
Facing difficulty speaking or seeing

With the occurrence of such symptoms, a person is advised to:

Get their glucose levels checked
Consume items that contain around or about 150-20 grams of carbohydrates or glucose
Wait for a duration of 15 minutes
Check your glucose levels again
Repeat in case the levels still come out to be low

If despite all your efforts the level remains low, you should seek medical advice. If you end up losing consciousness, you should prefer seeking emergency help.

In case of a high level of blood sugar

A person suffering from hyperglycemia or a very high level of blood sugar might notice symptoms such as:

Thirst
Headache
Frequent urge to urinate
Tiredness or weakness
Blurred vision

It might help if you regularly exercise. If a high level tends to persist, it is advised that you consult a doctor as you might need an adjusted treatment plan instead. Also, in case the symptoms in both situations are severe, you might want to go for emergency medical attention as well.

Monitoring the blood sugar levels

Monitoring the sugar level of your blood is a crucial part of managing diabetes. An ideal monitoring plan might include:

Test in the office of a doctor
Fingerprick test
A CGM device that monitors the level of glucose throughout a day

The time when a person generally checks his level includes before a meal, while noticing any related symptoms, or before bedtime.

A person might also go with additional testing:

Succeeding to the adjustments in diabetic blood sugar levels chart After, during, or before the exercise
During night
When he does not feel well

The frequency to get yourself tested tends to vary concerning the stage and type of diabetes you are suffering from along with other individual factors. A doctor will advise you on how often and when you should get yourself tested.

Conclusion

Management of blood sugar levels is a very crucial step to prevent diabetes and related complications in the future. If it stays within the recommended range, treatment is said to be working. Individual needs might differ; a doctor helps in setting up goals at the beginning of the treatment to cut you off from all the concerns about blood sugar levels.

Want to get access to the best training programs for business

StickyOscar

If you want to know about the multiple training levels then you can decide to participate in the programs. The set of the software tools is very useful for the users to learn the marketing strategies. You must ensure to perform the required research on the internet to get access to training programs. The educational materials are provided if you are ready to create your website. There will be many benefits for the users if they use the business model in the affiliate marketing using Entre Institute Review: The Best Training if You Actually Want to Make Money. It is appealing for many of the users if they are interested to make money online.

The successful strategies should be identified if you want to achieve success in the business.
You can get ready to manage your own business with the help of the management system.
The business model is useful for the users to focus on affiliate marketing strategies.
There will be many benefits with the software tools when they participate in the training programs.
The management software can be used effectively to set up your own business.
Professional marketers always provide the best guidance to the users about marketing.

Become a successful internet marketer:

If you are attracted to coaching programs then you can proceed to enter into web marketing. The courses which are offered by the professionals are very useful to improve your business. The mentors are always available to provide the best guidance about the courses. The reviews and ratings are useful if you want to find the best-rated programs based on Entre Institute Review: The Best Training if You Actually Want to Make Money. You can make money from the comfort of your home once if you become a successful internet marketer. The support and training provided the training programs so you can get started with the internet marketing.

Determine the position of your business:

The detailed instructions are provided so there will be no issues for the users with the training programs. The required guidance is offered to the users if they want to learn more about the business model. It is possible to determine the position in your business if you have the required capabilities. If you are interested to make money online then the training programs are considered to be very useful. The best advice is offered by the successful affiliate marketer so you can achieve success in your business. The online business is one of the best options if you are planning to create your income.

How to choose your favorite character with amazing visuals?

StickyOscar

It is possible to meet the expectations of the customers with the affordable range of the products in our merchandise. You can try to know about the latest updates about the products if you just subscribe to the newsletter on our website. The customers can proceed to select the products of their choice as there will be no limitations on our website. The products are available with excellent quality so the customers can proceed to make a purchase decision at our store. You can choose the payment method of your choice if you want to make payment for your kimetsu no yaiba figures. The amazing visuals are available for your favorite character so you can have the best purchase experience on our website.

The great poster hangings are available to meet the requirements of the clients.
The posters which are available on our store are very durable so you can use them for wall decorations.
You can select your favorite character in your realistic way as the products are available from the best suppliers.
There is no need to compromise on the quality as the accessories and costumes are available at affordable prices.
The one-piece costumes are available in different sizes so there will be many advantages for the customers.

demon slayer figures

Explore the huge product catalogue:

The slayer masks are available with quality cotton to meet the expectations of the clients. It is possible to match the look of your entire outfit with the products which are available in our merchandise. The huge product catalog will include several products so you can select the products of your choice. The best synthetic material is used to manufacture the Kimetsu no Yaiba figures in our merchandise. If you have any queries related to the other you can approach the support team on our website.

A great addition to your clothing:

The stunning images of your favourite character can be visualized with the products which are available on our website. The maximum protection can be ensured for the users with the perfect fit of the products. If you want to add a great addition to your clothing then you can shop for the products on our website. The best delivery options are available so you can receive the products directly to your doorstep. The best updates and reviews are very useful for the customers if they want to make the right decision at the right time.

Types of sleeping disorders

StickyOscar

Sleep is something which is a most important need for everyone. Without proper sleep, humans can suffer many health issues. Lack of sleep can increase your weight, loss of focus; you will not be able to maintain the right mood, and many more. But the sad part is all will not be able to sleep peacefully due to many different sleeping disorders. Sleeping disorder is the phrase used to describe when any person is unable to sleep or facing some trouble. In such a case you can use the best cbd for sleep which will help you to reduce the disorder. If a person does not get proper sleep it will affect them in the complete day and also at the night. Anything that may be the reason for not getting proper sleep is a health issue. Let us took into some of the common sleep disorders.

cbd sleep

Snoring: It can be the most common sleeping disorder found in humans. There can be many reasons for snoring. It is caused when a person faces difficulty in sleeping by keeping his\her throat open. Usually, when the throat muscles get relaxed they narrow down so, due to this the airway is closed. The snoring sound comes when the air is trying to enter through these closed airways.
Sleep Apnea: It is a medical condition in which the person breathing is stopped, due to a lower down of the oxygen level. The disturbance in breathing can be due to the upper airway getting blocked or the signal to the brain is failed to breathing. There are treatments available for this type of disorder.
Insomnia: Another common sleeping disorder found in many people. In this condition, the person will be unable to fall asleep and, if he wakes up in between then, he may take a lot of time to sleep again. If such a condition is happing regularly then the person must consult the doctor.
Restless legs syndrome: The name itself describes the condition of the type of disorder. The person will have some sensations feeling in legs. Like something is crawling on his leg or needle piercing. This sensation is reduced when there is some moment in the leg, like while walking or when the leg is stretched.
Circadian rhythm disorders: this disorder is caused when any person losses the connection with the external environment. This type of disorder can be seen in people who are blind or work at night. The disorder can be treated, by getting exposed to natural sunlight at a given specific time. This will help to connect back and get back to the normal sleeping order.

Conclusion

Finally, most people in the world face sleeping disorders. So it is important to keep a track of your sleep order so that if you feel any abnormality then you can immediately consult the doctor.

Enhance Your Testosterone With Best Testosterone Booster

StickyOscar

At present, men also suffer from low libido and reduced sex drive with the increase in age. They want the best solution to opt for to meet the sexual needs of them and their partners, as sexual activity is the necessity of everyone’s life to calm the mind and reduce stress. It will give the best outcomes with the best function.

However, due to plenty of options, it is not easy to judge the best solution that will work naturally in the body of a man. This is why experts recommend natural herbs to use when it comes to boosting the sexual drive and interest in men. These natural herbs are very helpful and also increase immunity fast. They are great to increase the testosterone numbers safely. These products are best and good for use. One can take advice from the doctor and go for it.

Ashwagandha: The best herb

There are many herbs present in the market like Tongkat Ali, Muira Puama, Tribulus Terrestris and a lot more. But among all, Ashwagandha is a highly-rated natural herb, which is claimed to boost the natural production of testosterone in the body. It is important to clear out that it does not have a direct impact on testosterone levels. Using this natural herb will nourish the glands, which are liable to produce hormones. It will give the outcomes in the enhanced optimal function. Moreover, after the herb is added to your body, the hormones typically get balanced, including the testosterones.

Order Best Testosterone Booster

When the testosterones are balanced in the body, a man will be able to achieve a high rate of libido as he has had at a younger age. According to the studies being assessed, it is stated that the natural herb is proven to work on the body in different ways. They have shown that several men worldwide have noticed a great increase in the T levels, which will lead to better and enhanced sexual performance and drive. Refer to best testosterone booster for more information.

Other benefits

Apart from increasing the T levels, Ashwagandha has other health benefits too. Some of them are mentioned below:

Reduction in the stress levels
Enhancement in the quality of the sleep
Better mood levels
Boosts strength and endurance
Raises the level of VO2
Enhancement of the cholesterol and blood pressure
Encourages the fat loss
Manages the overall weight of the body

So, if you are willing to use this natural herb, go online and find the best and reputed online store, where this herb is available at affordable prices. You can visit Best Testosterone Booster to get complete information about the relationship between Ashwagandha and testosterone.

Protect Your Life With Life Insurance Cover

StickyOscar

The family can now generate the monthly or annual income using life insurance. From the two-year to 25 year period, you can ensure your mortgage, funeral, or kind of debt with a lump sum by nominating tax-free monthly income because Aviva MyProtector, a leading insurance company, offers the option of a monthly tax-free advantage. See Aviva MyProtector Term Plan review and get the critical information about the life insurance policy.

Using the Aviva MyProtector online life or health insurance calculator, one can quickly obtain life or health insurance quotes. You can even measure your life insurance level with our calculator for life insurance needs. This gives you peace of mind that Life Insurance is the right amount for your needs.

Methods are available to find out how the premium for various quantities of life insurance cover is structured.

Insurance

What your smoking status and age are the main factors that depend on the policy. A calculator for health insurance is provided to help you arrange your Life Insurance requirements. Compare, select and apply in three easy ways online. The online insurance application has recently made it easier to use for life insurance.

The life insurance can be paid as a lump sum, which is tax-free.

Then the beneficiary can relax when debts, funerals, and other mortgages are paid with life insurance cover, such as returning labor or children who have left home for school to keep life financially.

The insurer has to be financially strong, as are many life insurers.

Fine product, policies, and application for a better life in finance and investment.

The protection of your loved one or those left behind in New Zealand can be obtained from life insurance companies, which can help the policyholder.

Not to be affected at the time of death by financial loss.

In terminal illnesses, some insurance plans offer a diagnosis based on the terms of the insurance policy.

It also protects you from debts and bills for those that are left behind.

Insurance

Joint life or one foundation.

In many cases where the principal member of the family dies, it is tough to cover mortgage and bills in various life insurance policies and schemes for children and others who cannot pay off or earn for their life expenses.

The primary objective should always be to maintain a healthy financial balance, and if you choose the right policy or cover, you can reach better financial goals. Instead of having complex funding needs, you have to make sure that you can invest, which returns the best to your money plan and requirement. It is therefore essential to know your premium structure before investing.

Various lifecycles can be chosen, and how the premium structure depends on different factors such as age and smoking habits. You can choose your premium structure based on your Life Insurance premium requirements.

Qualities of a Good Limousine Rental Company

StickyOscar

Since Limousine rentals are becoming more common and popular these days, lots of limo rental companies have been established in the market. These companies are trying to get their fair share of the huge Limousine market by providing their services. This has increased the competition manifolds, and has made an improvement in the quality of services while reducing the overall cost of limousine services.

If you are also looking to rent a Limousine for any occasion, you should look for certain qualities in a the Limousine company you are planning to rent a Limousine from. In this article, we will tell you about the qualities of a good limousine rental company which you should find before renting any vehicle from Napa limo rental .

A Large Fleet

One of the biggest qualities any limousine rental company can have is a large fleet of vehicles. This allows you to choose from a wide range of limousines, and you can Choose the Features you want installed in the rental limo.

So, always choose a company who has a large Fleet of Limousines available for rent.

Impeccable Customer Support

One of the most valuable features any limousine company can have is a good customer support. Customer support should be trained to behave well with the clients, and should be competent enough to help the customers in any emergency.

Good limousine companies are known for their impeccable customer support. So, you should always choose a company who has a good customer support.

Qualified Chauffeurs

Limousine Drivers make sure that you are transported to your location safely. So, make sure that the limousine company you are renting the limousine from has a good team of qualified Limousine Drivers with Clean driving records.

These were some of the qualities of a good limousine rental company.

Cleaning a Cut During a Limo Ride

StickyOscar

While you might not want to think of such things in the midst of a limo ride that would undoubtedly be filled with all kinds of debauchery, it is essential that you try to think about how you can implement various forms of first aid at this current point in time. You never know when you might end up suffering from a cut while you are riding in your favorite limo of all time, but this doesn’t mean that you need to let the cut get in the way of you making the most of things.

What you basically need to try your best to understand is how you can go about treating a cut during Phoenix limo service, and one way in which you could go about doing this type of thing would be to look into cleaning it up so that it doesn’t get infected at any point in the future. You probably have alcohol on your limo, and as a result of the fact that this is the case using alcohol can be something that you can do pretty easily without having to worry about anything else at all.

Alcohol is going to burn when you apply it to your cut but this is a good thing because it means that it is getting the job done. Once the cut is cleaned you can bandage it up pretty easily, and subsequently you wouldn’t really have to worry about anything else at all. This proves that first aid in a limo is all about making do with the various things around you as best you can, and there will likely be something or the other that you can use.

Is it possible to grow your muscles with muscle hypertrophy?

StickyOscar

High-quality proteins are always required to boost muscle growth in your body. The by-product of milk processing can be obtained with a fast-acting protein called whey. You must ensure to train your muscles regularly when you use the protein powders. If you want to boost muscle hypertrophy then you can grow your muscles without any issues. You can decide to use the premium form of the best protein powder for gaining muscle even if they are a bit expensive. The processing and refinement are done effectively to isolate the whey protein. It is possible to break the bonds between the amino acids as the whey protein is heated with special enzymes.

Instant fueling is offered to your muscles within 15 minutes of consumption.
The incredible substances are very useful for the individual if they want to reduce muscle soreness.
If you prefer to use the supplemented groups then you can reduce the muscle pain significantly.
The delicious flavors of the protein powders are available so you can choose the flavors of your choice.
The best ingredients are used in the protein powders so you can have a satisfying drink.
The free shipping facility is available so you can receive the best protein powder for gaining muscle directly to your doorstep.

Promote the growth of muscles:

You do not hesitate to purchase the products as they are available at affordable prices on our website. If you want to find the big improvements in the strength gains then the protein powder is considered as one of the best options. The growth of your muscles can be promoted effectively if you are impressed with the results. If you want to find the best look then you can stretch your muscles after using the supplements. The best protein powders are available for muscle building so you can feel free to approach our team.

Ingredients used in the products:

You can proceed to purchase the supplements without any obligations by reading the reviews on our website. If you want to know about the ingredients used in the products then you can just check out the description. A huge number of reviews can be found by the customers when they just visit our website. The great results can be experienced by bodybuilders if they use the protein powder daily. The terms and conditions of our website should be verified by the customers if they want to make a purchase.

Get some discounts on your purchase:

The incredible ratings can be explored by the users to find out the protein powder which has a great taste. The customers can enjoy the free shipping when they have a look at positive reviews from the trusted company. If you want to get some best discounts during the time of purchase then you can visit the official website. The premier online venues are very useful for individuals if they want to enjoy the best benefits. You can provide your valuable feedback if you are satisfied with the results obtained with the products.

Let us talk about PhenQ’s ingredients

StickyOscar

Like any good supplement company, PhenQ advertises the specific ingredients they use with absolute confidence. We’re going to list what they are and their effects to better inform you of the product.

Capsicum Extract

Capsicum Extract, which comes from certain peppers, such as chili peppers. It has thermogenic properties, which boost your body heat, which has a couple of effects.

The main thing this does is boost the rate at which your body metabolizes fat and conducts other metabolic processes, which are already quite good. However, on top of this, it also has appetite-reducing properties, making it easier and more convenient to eat less food.

Caffeine

Caffeine, which as we all know, is a commonly found natural stimulant. In other words, it boosts mental clarity and energy levels, as well as boosting the rate at which your body does things.

Now, “things” is quite broad, but think of it as having a similar effect to increasing your body heat, though with less fat-burning properties. In addition to this, it can help suppress your appetite as well.

Vitamin B3

Vitamin B3, also known as Niacin, helps convince your body to burn food for energy instead of keeping it around as stored adipose tissue or fat. This effect works better if you exercise; even taking a walk can help boost the effect of niacin to better help you lose weight.

Of course, it can increase hunger because your body will burn through food quicker, but that’s where the other ingredients’ appetite suppress properties come into play.

Piperine

Piperine, which comes from black pepper, is another compound with thermogenic properties, meaning it raises your body heat and helps burn fat. On top of this, it has other beneficial properties. First off, it may help prevent the formation of new adipose tissue cells, and second, it can help regulate obesity-induced dyslipidemia, a condition where you have an abnormally high amount of fats inside your blood.

Chromium Picolinate

Chromium Picolinate, a compound found in all sorts of foodstuffs, can help control your desire for carbs and sugars, which can help regulate blood sugar levels. It does this by increasing cellular sugar uptake, which, again, reduces cravings for carbohydrates.

Nopal

Nopal, which has a high fibre content. Fibre can do a couple of things for you. First, it aids in regular and normal bowel movements, and on top of that, it increases how long you stay full after you eat.

Nopal cactus, itself, has its own benefits, such as having a large concentration of essential amino acids and helping to cut down water weight. Those amino acids can help boost a lot of health factors, but primarily they’ll work on increasing energy levels.

L-Carnitine Fumarate

L-Carnitine Fumarate, another compound commonly found in food, is an amino acid that aids the burning of fat to produce energy. This can help make up for the caloric shortfall caused by dieting with the goal of weight loss, burning fat stores to keep the rest of your body working optimally. It can also help boost energy levels!

Calcium Carbonate

Calcium Carbonate, which is good for your bones and is a chemical messenger. Calcium carbonate, when it contacts the brain, tells it that the body is full up on fats, and it should get to burning fat. Your brain will also suppress appetite to avoid wasting food when you already have enough fat to burn at the moment for energy and nutrients.

α-Lacys Reset

α-Lacys Reset, which is a combination of other compounds and an element, namely Alpha-Lipoic Acid, Cysteine Base, and Magnesium. These three, working together, aid metabolism and thermogenesis, or increasing body heat. These two factors, as discussed previously, boost fat burning in the body by quite a bit because the fat is what is burned for heat.

Reliable Outlet for Quality CBD Products for Dogs

StickyOscar

There are several evidences proving the reliability of CBD oil for treating series of ailments in humans. There are also evidences to prove that even your dogs can benefit from the use of CBD products. You can get CBD products over the counter and this makes it easily accessible. There is no need for a doctor’s prescription to buy it. The use of CBD products is also legalized in the United States. So, there is no fear of being on the wrong side of the law when you use it for treating ailments or give it to your dog. CBD oil gives a 100% natural solution to ailments and this means that you will never have to bother about side effects when you use it. Your dog will also not record any side effect for using CBD oil for dogs.

Reliable place top patronize

You will find so many outlets selling CBD products out there today, but you should not pitch your tent with any of them until you have properly investigated them. You should take some time to read reviews about that outlet to be sure that it sells quality CBD oil. If you reside in the United States and you are looking for a good place where you can buy quality CBD products, then you should head over to Glow CBD and it will turn out to be one of the best decisions of your life. Check below for some of the many benefits of patronizing this outlet for CBD products.

THC-free products

THC is the acronym for Tetrahydrocannabinol. This is the psychoactive component of cannabis and it can get you “high”. This characteristic makes it unacceptable in the medical world and many governments have banned its use. So, any CBD product that contains THC is illegal. It is unfortunate that many of the outlets selling CBD oil for dogs sell CBD products that are tainted by THC. This is never the case when you purchase your CBD products from Glow CBD. The outlet sells pure CBD products that are free from THC. So, you will not be on the wrong side of the law when you buy your CBD oil from this outlet.

Everyone is welcome

You can get CBD products for dogs at this outlet hassle-free. If you have a cat, on the other hand, and you want the cat to benefit from CBD oil, you can equally shop for CBD oil for cats here. Aside from pets, the outlet also sells CBD products for humans. While purchasing CBD products for your pets here, you might as well order one for yourself. We can, therefore, call Glow CBD your one-stop shop for CBD products.

How to use it

The CBD products sold at this outlet can be purchased without a doctor’s prescription. Be that as it may, you should be responsible while using the products. For one, none of the CBD products sold here should be used by humans younger than 18 years old. Additionally, you should always follow the directions on the labels when using the products. Make sure you consult the vet doctor before using the CBD oil for your dog or cat.

Let’s Check Out the Triple Benefits of Hemp Gummies

StickyOscar

Daily wear and tear can lead to knee discomfort or even arthritis. It can also be caused by an unbalanced meal plan or a diet that does not contain the nutrients your body needs to keep fit. Degenerative joint diseases such as osteoarthritis can affect people with varying levels of discomfort, and unfortunately there is no cure for them. Many people try to control their discomfort with pain relievers or non-steroidal anti-inflammatory drugs, or more generally described as NSAIDs.

While pain relievers and NSAIDs relieve discomfort, they do nothing to fix the root of the problem. They just mask the problem and don’t help the body fix it. A much better option is to use hemp gummies that can help your body repair damaged joints, thereby minimizing discomfort. Another great fact about using hemp gummies is that they generally do not have dangerous negative effects. The same cannot be said for pain relievers and NSAIDs.

Hemp gummies – what is it?

One of the best ways we can help our body repair itself and repair damage over the years is to provide it with the nutrients that are normally produced and that our bodies are currently using. In this case, it is a CBD product called hemp gummies. Hemp gummies is a natural CBD product. Hemp gummies is a CBD product that is formed as a result of the inclusion of a number of other nutrients from the hemp tree. Hemp gummies acts as the building blocks for cartilage located in joints. In particular, hemp gummies is essential and important for maintaining joint health.

Over time, as we age, our bodies begin to produce less energy. When the production of energy in our body is reduced, our body’s cartilage cannot fully recover from daily tasks. These daily tasks can be simple things like walking, running, or grocery shopping. Whereas we have to do these kinds of tasks every day, overtime work, if you allow your joints to fail, can deteriorate and result in inflammation. When this happens, the joints can rub against each other, causing friction in the joint and, ultimately, severe discomfort.

How can I get more hemp gummies?

Thanks to modern science, scientists have discovered a way to make hemp gummies that help the body produce vitamins and fatty acids. The best form of hemp on the market today is hemp gummies. It’s a little more expensive, but has been found to give much better results than the less expensive hemp products. In addition, your body absorbs hemp gummies faster, and therefore, important nutrients are much better distributed throughout your cells.

NSAIDs and pain relievers only relieve discomfort and do not eliminate wear and tear on weakened cartilage. Some can also have serious negative consequences. Some negative effects were enough to make a few products recall. Hemp gummies address joint problems by helping the body repair damage. Hemp gummies are usually combined with other nutrients. Hemp gummies are an effective combination that helps more people with joint discomfort every day.

Living a Beautiful Legacy: What and How?

StickyOscar

Many people desire to have a great legacy that they will leave behind when they leave the earth. That legacy is a lifelong journey that they should decide someone to take in every day of their lives.

Nowadays, many individuals have found how they want their legacy to be known by their families and other loved ones. If they are now working with it, there are still out there who are looking for the works they desire to do. Surely, many people can relate to this reality because of the changes that happened in society throughout these years that went by.

Is anyone here thinking of their desired legacy here on earth?

For the younger ones, it is not something that they are focusing on already. It is not the same case with the elders and adults who have reached a certain age and have started to think about their desired legacy. It is because they realized the life they went through as they aged.

Living A Beautiful Legacy

Those people who are thinking about their legacy surely realize things in their lives and things around them. Surely, those who are not are now finding it through stating to know how they will live with a beautiful legacy.

The simple answer to that is to engage with the works of God, which the scriptures say. It is the great teachings at Shincheonji Church of Jesus, wherein the Holy Words say that every word that came from God will come out with pureness and joy. Besides, there will always be compassion that will come from a person who is full of the words of God. Surely, every work that he or she will desire to do will be full of love and care. It is because the powerful words of the Almighty fuel the intentions.

The Great Role of the Church

The Church of Jesus mentioned above is the home of people who are anointed with power and greatness. It is because of their knowledge of the truth about Jesus and His great works. That is why it is not a surprise that it is easy for these people to work for people with nothing in return. That is how amazing this truth is, which is already discovered by these beautiful people.

The church’s role in providing the truth to those in the middle of their crisis is huge. Because it has the power and capability to change one’s life and make it new again, it means there will be new desires and perspectives that will only come from God. Surely, those intentions are all beautiful. It is because they started to see, feel and know how blessed they are. As soon as they realize it, they will surely desire to become a blessing to other people. As easy as that, everyone will be starting to live a beautiful legacy here on earth. It might not be an easy journey, but it will all be worth it. Because at the end of the day, what will matter the most is the memories and impact that anyone left on their loved ones.

Bring Forth Working Electricity on Your Dark Camping Nights

StickyOscar

Camping is an activity that you would typically do in the middle of the woods. Although there are some predetermined campsites out there that people can freely use, you still expect to be outdoors for the remainder of the camp trip. The entire purpose of a camping trip is to be out on the great outdoors with your fellow friends and family. As such, you should prepare to be away from civilization and electricity for most of the trip.

An entire camping trip that forces you to stay inside and use various technology devices would beat the purpose of camping. But there are some basic functionalities that electricity can make the situations such as emergencies easier to manage. One prime example of a problem where you have to consider the benefit of electricity would be the lighting. It is incredibly dark when it comes to dealing with nature at nighttime. As such, a couple of small lamps here can help make the entire experience feel more comforting for some people.

Fortunately, you can make sure that your campsite has ample electricity without becoming a focal point of the entire trip. All you need to do is get your hands on the best portable generator super quiet device, the WEN 56200i Generator.

Light in Weight, Heavy in Capacity

The great thing about these portable generators is that you can use them in almost any situation that requires electricity. There is no point in dealing with various issues that requires a constant stream of electricity since your portable generator can charge virtually any device out there. You can set your phones, power up some lights, and even use this device as a way of messaging emergency services for help.

One of the significant downsides of portable generators is that they can take up quite a lot of space, be noisy to use, and bring a ton of weight to the party. However, you can bet that this specific model is one of the best in the market. With a combination of noiseless engine and extremely light carrying capacity, there is no reason why you should not jump in and start purchasing this product for all your future camping trips.

You can get your hands on this particular device today by heading on over to the forCampingGear website and purchase one today. There is an included warranty for those that worry about the quality and longevity of this device. However, you can rest easy knowing that you can take this device almost anywhere you go, and it would still hold up through the times.

The Importance of Using Thermogenic Fat Burners

StickyOscar

While there has been a push to improve your body in recent years by exercising and eating well, the sheer amount of food and activities you can do while sitting is distracting. Of course, when there is a need, something fills the gap, which is why weight loss supplements have been introduced to the market, the best fat burners are thriving. However, it is essential to know which supplements can help you and which can seriously harm your organs.

Thermogenic fat burners

These supplements are designed to burn fat without moving additional muscles. Some argue that they increase your metabolism so that your body can burn fat in due time, and some say that they optimize your body to burn fat cells. The idea is that a fat burner helps you lose weight quickly so you can be the slim and sexy person you’ve always wanted to be. While some of these products are effective and you shouldn’t waste your money, some of them may help some people lose fat. Perfect examples of this are the natural acai and maca berries, which are rich in antioxidants that can help you lose weight and help maintain your health in other areas. There are also chemical fat burners that are not suitable for many people, but they can help you lose a few pounds a week if supplemented with exercise and the right diet, click https://www.westword.com/storyhub/best-thermogenic-fat-burners to learn more.

Appetite suppressants

While they won’t help if you are eating, hungry or not, they are great tools for those who are always hungry over food. It is another all-natural supplement that contains a molecule called P57 that helps you feel full when you eat and helps control your cravings when you are not eating.

Binders and fat blockers

Unlike traditional fat-burning foods, they help you lose weight by literally blocking the body from absorbing a lot of fat from what you eat every day. Instead of being absorbed, fat passes through your body as undigested food and dissipates in your stool. The most significant disadvantage of some of the more popular fat blockers is that if you eat fatty foods, you should wait a bit before getting in the bathroom because most of the fat will pass through your body.

In the end, which path to take when it comes to weight loss supplements is entirely up to you. Be sure always to remember that all of these remedies are helpless if you do not eat properly and exercise regularly; There is no way around these requirements, but if your body needs a boost, try a thermogenic fat-burning supplement today.

Bodybuilding supplements can be quite tricky to understand because many of the ingredients are difficult to understand. Many supplement companies use labels that hide the actual amount of components. Only by reading professional reviews of nutritional supplements will you be able to understand which supplements to purchase.

Summary

If you want to burn fat, there is no substitute for a healthy diet and regular exercise. Proper use of thermogenic supplements, combined with exercise and adequate nutrition, can have a potent fat-melting effect.

Ramps for wheelchairs and how to choose one

StickyOscar

Many people use wheelchair ramps or electric scooters because they cannot stand for long periods of time or because their legs do not function properly. Put, wheelchair ladders are inclined planes that make it easy for wheelchair users to get to their homes or other buildings. Getting in and out of your home or business is something many take for granted. The slope of these ramps is important because certain angles are tough to maneuver from a wheelchair. Both portable and modular ramps take this into account in their design. Standing slopes, whether modular or made of wood, should be designed with this in mind. Laws have been put in place to help protect rampe handicapé users when companies install ladders, ensuring that the ramp is within specifications.

When considering building a ramp for a disabled person, these things should be kept in mind:

Ramp function

Each person’s disability is different. The function of any wheelchair ramp is only useful if it is designed with them in mind. Since people with disabilities use these ramps with different capabilities, such as entering and exiting vehicles, entering buildings, or reaching entrances to public places or even streets, it is necessary to consider their needs.

Slope size

Just as each user of a wheelchair or scooter differs, each of these modes of transportation has different specifications. You can find these measurements in the manual or on the inside pages, but the recommended ratio is usually 1 to 12 for businesses. Every inch of the slope requires one foot of the slope. The recommendation for a home is 2–12, which means every inch of the slope requires one foot of the slope. Scooters require a ratio of 3 to 12. To build a ramp, you need to measure the length of the ladders that need to be covered and calculate accordingly.

Types of slopes

There are several different types of rampe handicapé, including portable, modular, wood, and compound ramps. Portable ramps can be folded and taken with you and are usually used to overcome smaller obstacles, such as a pair of entry ladders. It’s solid and makes going to new places so much easier. Modular slopes are durable and made of aluminum, so they are long-lasting. Although it is “permanent,” it can be transported. Because it is made of aluminum, it does not crack. It comes with handrails and is quick to install, although the best fitting is by a professional. Wooden ladders are old ramps for wheelchairs.

They are durable and difficult to move without damaging them. They may or may not have handrails, although handrails and edge rails for wheelchair and scooter users should always be installed. Vehicle ramps are used to facilitate entry or exit from a vehicle and are mounted to the side or rear of a truck or large vehicle. If you need to install a wheelchair ramp for a school or company, modular ramps meet American standard recommendations and are a smart investment, as they don’t need to be painted or treated.

Qualities a person needs to run a business

StickyOscar

People prefer to run an own business than going to a regular job every day. There are several reasons that people may decide to start a business. But to become a successful entrepreneur, one should have all the right qualities. Running a business is no easy task. To maintain a successful business one need to have a practical business plan. Successful entrepreneurs know what business is right for them. They have the ability to market the business and implement financial goals. Check about the business details by clicking here https://masakor.com/include/category_view2.php?area1=20190405173807_3123&category1=, the business that helps to keep the people healthier. Below are some qualities that you should know before you decide to run a business.

Entrepreneurship:

Entrepreneurship skills mean possessing the determination and commitment to run your own business. To become a successful entrepreneur one should have organizational, sales, marketing and finance skills as well. Many business owners have the natural talent for entrepreneurship. Some develop these skills with years of experience.

Personal Traits:

To run a successful business one need to have many skills that include decision-making skills, interpersonal skill, and self-determination. These traits are linked to the ability to run a business.

Various business types require various skills. The business included in this website https://masakor.com/include/category_view2.php?area1=20190405173807_3123&category1= requires special skills. One needs to have patience, and able to listen to the problems of the people. Only after identifying the problems correctly, they can give the right services to the people. Being able to work well is an important characteristic that a business owner must have.

Business management:

No matter the type of business, problems may arise at any time. Having the ability to manage the stress of deadlines, employee relations, and any unexpected stressful situation are all part of possessing management skills. Another major aspect to consider is the changes in technology and industry trends.

Creativity:

A successful entrepreneur has a creative passion to establish the business that is right for you. Using creative ideas and implementing the right working ideas can help one embark on a successful business venture. People always prefer a business that uses creativity and provides services in the best possible manner.

Common questions about crypto arbitrage

StickyOscar

The people who are into the cryptocurrency trading and the people who are dealing with cryptocurrencies would have known about arbitrage. This is concept of making profit by buying and selling the cryptocurrencies from different exchanges. In this concept, the traders will make use of the ups and downs in market and will play the game according to it. But it is to be noted that the traders must make a better move in order to make profit out of their attempts. Even though this concept is highly followed by many traders all over the world, still there are some beginners who tend to have hesitation in making use of it. Some of the most common questions about this arbitrage are revealed here.

Is it legal?

Almost all the people who are coming across this concept for the first time may not be aware of its legal status. To reveal the fact, there are many people who think that it is highly illegal. But this is not the fact. The concept of arbitrage is completely legal and hence the traders can make use of it without any constraint. At any extent, they will not be put into any kind of legal issues.

Is it profitable?

Undoubtedly, it can be said that crypto arbitrage is profitable for the cryptocurrency traders. But as mentioned above, the traders should be capable of using the ineffectiveness in the market. The people who have the capability to make quick and effective decision can earn a better profit out of arbitrage. There are some people who fall under the category of day crypto trader. This kind of traders can make some limited profit out of arbitrage. The traders who buy and sell in different exchanges can also make more profit but in case if they fail to deal it in the right way, at times it may be ineffective.

How about storing coins?

One of the most important questions raised by many traders is about the storage. Since they will be in need to access more number of exchanges for this trading, they may be in need to take control over all these factors. Since all the cryptocurrencies will be under one account, they are supposed to be more careful. This is because there may be possibilities for hacking and other online threats. Hence the traders are supposed to get established in the limited number of trustable exchanges which has the best online security aspects.

How to make the calculation?

Since the traders are supposed to make better profit, they are supposed to make better calculation. One of the most common mistake done by many traders is they will not include the transaction fees in their calculation. The traders must remember that while accessing each and every exchange they are supposed to pay certain amount as transaction fee. Hence while formulating the profit, they must take it into account. That is they must decide the profit by including the transaction fee and other expenses they have invested.

Features of USA’s Best Mobile 4G LTE Proxy/VPN Networks

StickyOscar

These days, it is important to be private, especially regarding your online interactions and transactions. It is a known fact that hackers can easily have access to the information you share online without you knowing. They will know what sites you access. That is why you should invest in an excellent mobile 4G LTE proxy/VPN network.

One of the most trusted names these days is ProxyGuys. They have the best products and services to help you add a layer of protection to your online interactions. But before you buy USA 4G Proxies from ProxyGuys, here are the essential features you need to consider.

Accessible in Various Locations

One of the essential features of the mobile 4G LTE proxy/VPN from ProxyGuys is that you can access it in most US locations. The company has true LTE proxies/VPNs in more than 25 states and cities in the US. Each location will have a unique IP pool of 600,000 to 900,000 addresses.

Premium Speeds

Nobody likes delays and buffering. At ProxyGuys, the proxy/VPN they offer has an average speed of 50Mbps. Faster compared to other providers in the US. The speeds are stable, so you will not have to worry about fluctuating connections all throughout the day and all-year-round.

Change or Keep Your IP

When you choose to purchase 4G proxies at ProxyGuys, you will be given an option to keep your IP or change them. You can use your current IP for as long as you want. If you’re going to change it, there’s an option for you too, and you will get a new one in as fast as 10 seconds. There’s no time for waiting at ProxyGuys.

Information Provided Are Private

Some people are afraid of purchasing proxies and VPNs because they do not want to share their information. It is normal to be wary of providing data these days, especially online, but at ProxyGuys, you are assured that the company does not keep or store any logs on their proxies and VPNs. It means that your information is secure and will never be leaked.

Auto-Rotate IPs

Do you want to change your IP address once in a while? If you do, then you should consider the products offered by ProxyGuys. They will let you automatically change your IP as often as you need. You can set this up at their Multi-Location portal to let the system know what interval you need your IPs rotated.

Reliable Live Chat Support

You would never want to be left hanging if you are having problems with your proxy or VPN. That is why ProxyGuys ensure that you receive 24 hours support seven days a week. They have a live chat system here with real USA-based agents. Assistance can also be offered through Skype, Telegram, Slack, or Discord.

These are just some of the many features you can enjoy if you choose to purchase 4G proxies from ProxyGuys. So what are you waiting for? If you know that this is what you or your company needs right now, go ahead and visit their website to find out your options.

Differences Between Organic Coffee Beans And Regular Coffee Beans

StickyOscar

A Whole Lot of pesticides Have Been used in conventional coffee production. Normally, coffee plants have been treated with pesticides prior to harvest to protect against insects and fungus. After being harvested, conventional green coffee beans have been treated with a lot more compounds in addition to the aforementioned pesticides.

Long ago, coffee has been developed in organic surroundings under shade trees at which the plants can grow without interference. Now, largescale coffee plantations have abandoned this system and rather cut trees down and plant coffee in large clear cut areas. The shift in methodology has now caused the demand for fertilizers and pesticides to make sure they can keep producing coffee. The compounds by which coffee plants have been treated invisibly to the bottom and change land quality in addition to the caliber of the coffee beans.

Organic coffee beans, such as roasted by Nectar of Life, have been grown in a totally different way. Organic coffee is shade grown and mulching is used instead of chemical pesticides. This, and also using birds to control pests, eliminates the need for harmful compounds and is popularly called organic green farming.

The USDA includes a group of criteria for organic foods and also in order to get a commodity to become certified to be organic, it has to satisfy with the USDA’s regulations. Organic coffee drinkers shouldn’t use artificial dyes and has to rotate their plants several years to conserve soil nutrients. All of this is the way crops were grown in the past prior to industrialization.

Though organic coffee is generally grown on a smaller scale compared to conventional coffee and its own farmers must stick to strict USDA Tips, the fee of organic coffee is obviously, yet maybe not surprisingly, greater compared to purchase price of standard coffee. Bear in mind when you’re choosing seeking out a new organic coffee to purchase. In addition to the increased cost for certified organic coffee there is an additional cost if you go Fair Trade. We recommend purchasing coffees that are certified both organic and Fair Trade. This way you know you’re buying a chemical free coffee that earned the grower a fair wage.

Taking Sport Photographs Tips

StickyOscar

Taking sports photos is very easy and you can take some really good photos of them. If you really play sports and enjoy watching or even participating in games, taking sports photos can be a lot of fun and rewarding.

First, taking sports photos is not the same as enthusiastic parents photographing their children. Sports photos that look good don’t just indicate action and take them. If you look at most of them, you can see how they end up being very different from most of the sports photos that shooters take and the usual shots.

Sports photography can be quite difficult, especially if you don’t know how to do it or have slow eyesight. Most sports are very fast and contain a lot of movement. However, it’s easy to beat and take really great photos. If you can learn to capture movement smoothly with your digital camera, you can take really great sports photos.

When it comes to capturing action shots, be it sports photography or bird photography, there are some general tips. These tips are NOT just for sports photography. You can use these tips to capture action-packed photos of birds, lions, airplanes, and more.

One of the most important aspects of sports photography 먹튀 is your camera settings. If you’ve ever taken sports photos with a fully automatic camera, you’ve probably deleted almost half of the photos. Shutter speed is a parameter that is often manipulated a lot when taking dynamic sports photography. Another parameter that is often manipulated in sports is the ISO setting.

Exposure control

When you’re photographing any moving subject, the need to freeze the subject or blur it is entirely achieved at the expense of shutter speed. If you are shooting high-speed sports videos, you should stop the motion and have no blurred objects. This means you need a fast shutter speed. The shutter speed must be faster than that of moving subjects. If you are shooting a very fast subject, you will need a much faster shutter speed than a subject that is moving slowly like a turtle.

ISO settings

What happens when you use a faster shutter speed is that less light enters the camera. This may be fine for faster shutter speeds, but higher speeds require some ISO settings to allow for more light exposure.

Taking sports photos indoors can be much more troublesome. Since the light is mostly artificial, it will be much more difficult to expose correctly when controlling the shutter speed. When shooting sports photos with an ISO of about 400 or higher, that’s fine. Be careful when using ISO because using a very high number can make the image very noisy. A little noise is fine as you can easily remove it in photo editing programs.

In addition to settings, the equipment is also used for sports photography. If you are not allowed to be on the field with the players and not take close-ups of them, you are most likely a long way from the action. To get closer, you will need a high-quality telephoto lens. A telephoto lens is what all professional sports photographers use; it allows you to get as close as possible and take great shots of the action.

What happens with such long telephoto lenses is that the background is blurred. Shallow depth of field is common when capturing sports images and even sports broadcasts on television. If you take a closer look at the shots of individual players, you will notice that the background is very blurry.

Weather-Sealed Garage Doors: How To Do It?

StickyOscar

To have an airtight garage door is easy. You need to know the right tools to do it and the right materials to use. If you have noticed dirt, rodent droppings, or water in your garage, then it is easy to trace the problem by checking your garage door. Garage doors are huge, and while all come with a seal at the bottom to keep out dirt, water, wind, and even unwanted intruders, the seals may also break down for some time. A more severe case is that the concrete floor, as well as the driveway apron at the bottom of the door, can settle, crack, or shift, creating large gaps, which the standard seals can’t even cover. Garage Door rubber Sealing is a weather-sealing type. It has a simple process of the following:

● Replacing or adding the bottom door seal

● Weatherstripping the stop molding of the top and sides of the door

Also, it may include adding weatherstripping in between door panels. It is done when you want an airtight door as much as possible.

Different ways to seal garage door

There are 5 ways to weather seal a garage door. A do-it-yourself weather-sealing is possible if you have the right materials to use. However, if you don’t have any idea how to do it, you can ask for the help of weather-seal installers near you. For the different ways of installing a weather-seal garage door, you have the 5 ways here:

● Garage door bottom seal. The door sweep, garage door bottom seal, is a long rubber strip or vinyl attached to the garage door’s bottom edge. When the door closes, the flexible material gets compressed, it seals the gap on the floor to prevent water, dirt, critters, and cold breezes from entering. Once you see the daylight below, then it is the perfect time to replace the bottom seal.

● Garage door threshold seal. A type of seal with a similar function to the bottom seal. But, it is attached to the floor and not on the door. The threshold can be installed alone or with a door seal. It is often used for keeping the surface water slopes down towards a garage. Plus, it fills the large gap below the garage door. It can be a more durable seal. It is installed with adhesive. Threshold blocks water and keeps it from flowing.

There are a lot of ways to keep your garage safe from weather conditions. All you need to do is to check the entire garage space. If you are seeing any space where water, dirt, or any intruders, garage door rubber sealing keeps it out from happening.

Why choose rubber sealing?

There are a lot of options when you seek a good garage door sealing material. However, the challenging part of seeking a durable and easy-to-install weather-sealing garage door. Now, how can you compare the quality to a durable seal? Both are good criteria, but you can find them both in one material, which is rubber sealing. Rubber is water, mold, dirt, and any weather resistant. Meaning, the material can withstand any weather condition. So, if it is raining outside, you can have the assurance that water will never leak or enter inside the garage.

Top 5 You Should Learn to Pick A Betting App

StickyOscar

Betting apps are very prominent nowadays. People love the convenience and the effortless fun that betting can offer. Aside from that, some people also make a living out of it. Some people do gambling and betting to have revenue. In terms of this, there are plenty of betting apps that you can find online. Before you delve and play, you also need to ensure that you are on the right betting app. With this, you can gain and profit more out of it. Learn the top 5 things you should know about betting apps.

User Interface Design of the website

User Interface (UI) web design is all about how a website has good quality graphics and organized content. Seeing an on-point UI design means that the developers gave plenty of time designing their website before releasing it to people. It makes it easier for people to understand the objective of the betting app. Thus, it is vital to have a well-developed UI design. With this, you can assure yourself that the developers can commit to the services that they wanted to offer. Hence, they do not only think of gaining but let people have fun on their website.

Note the User Experience Design

You need to observe the gameplay of a betting app. After confirming your web design, move on to the UX design. Betting apps usually have plenty of games at hand. With that said, there may be some games that may have errors and bugs. A good User Experience (UX) interface hinders errors and bugs from happening. Also, it allows the user to experience understandable and concise instructions. You can confirm that the site is a good betting app you can trust once you have experienced the feel of this matter.

Has come to legal terms

There are no excuses that you need to have a license if you want to operate your business legally. It is a requirement that business owners and companies undergo a thorough investigation. Once they pass and acquire the necessary document, then all is good. People tend to trust websites with legal terms at stake. It is vital to ensure the safety of their players. More so, for the website to gain recognition. With this, you are setting a competitive environment in your gameplay from the betting app itself.

Competitive grounds of gameplay

The plausible betting app ensures that their customers will not have a dull time playing. Hence, they put plenty of games that players can indulge in playing. With that said, go for a website that has a competitive environment. The more adrenaline you feel, the better the gameplay usually takes place.

No bogus transactions

There are plenty of scam cases happening in betting apps since it is online. Ensure to be on a website where they have partnerships with known banks in your area to ensure easy withdrawal and deposit transactions.

With all that in mind, you can check this site and see the best betting websites for you. Never worry about scamming anymore. With APPMODO, they assure you to have fun and be safe in online gambling.

Learning What Takes Place in the Vape World

StickyOscar

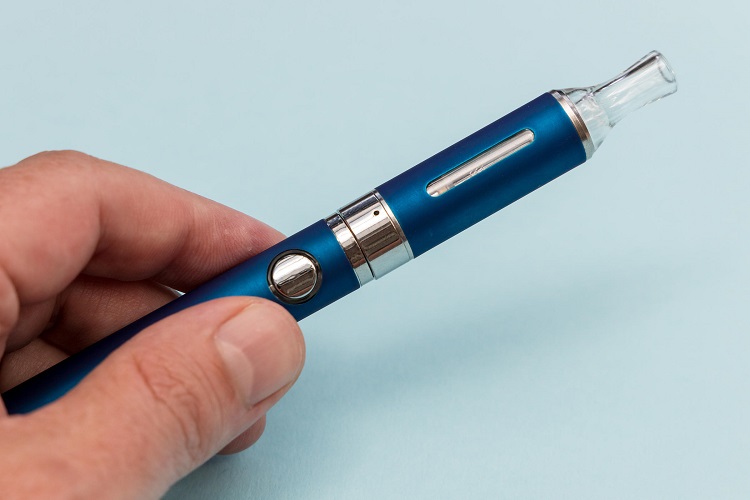
Vaping is the process of inhaling the vapors produced by personal vaporizers or electronic cigarettes. Electronic cigarettes are battery powered devices that may or may not contain nicotine. Heavy smoking includes large amounts of tobacco and nicotine, which can damage sensitive lung tissues and fill them with leaks, leading to permanent and irreversible lung damage. There are opportunities to eliminate persistent smoking habits by adapting to a clean lifestyle, eating and breathing healthily, and trying methods with less nicotine smoke, such as vaping methods. The world of vaping embraces everyone who wants to get rid of this terrible habit with outstretched hands.

Here’s a quick guide for those who don’t know what vaping is.

The technique is pretty simple. The e-juice evaporates, and the vapors enter the inhalation system through cigarette sticks, pipes, or handles. Among the kits, there are e-cigarettes, pens or sticks, e-vaping containers, e-liquid bottles, etc., for everyone. There are also smoking cessation kits and starter kits to make it easier for people to use and help them.

If you start vaping to quit smoking, you need to start with a commitment to yourself. The e-vaping technique has many benefits. Firstly, they do not come out with sequels. Second, they do not cause bad breath after impact. Then they can be bought and used inexpensively. You can also try different flavors like apple, cinnamon, blueberry, banana, etc., and choose which one suits them perfectly. There are also smoking cessation kits with these voopoo techniques to help you stay clean.

If cigarettes are bad for your health, the ends of cigarettes are bad for the environment. They leave sediment in the lungs, blood vessels, teeth, and in the mouth and hands of a person. Instead, these vaping methods leave no trace anywhere. One of the biggest benefits of subscribing to a vaporizer kit is its less toxic nature. E-juices contain lower levels of nicotine and organic flavors, which reduces the need to smoke regular cigarettes. Gradually, moving to vaping technique, the heavy smoker also feels better and can lead a quality life. The great thing about vaporizers is that they have many modifications that you can customize as you like.

These are some of the advantages of using an electronic vaporizer over traditional smoking. Electronic cigarettes and pens are easy to use, maintain, clean, and refill. They are also environmentally friendly as no residue remains. So guys, go to the world of vaping where you smoke without harming yourself or society. It is a healthier alternative to smoking; it’s the next cool thing in town; You should try it too; it is much better than smoking; it is more profitable than smoking. Chances are, you’ve heard all of these words from people in your social circle. Vaping is the next big thing for all nicotine lovers and represents a healthier alternative to smoking at nearly half the cost.

Summary

You should only purchase your vaping device from a branded company to ensure its quality. Take a short survey to get a clear idea of your services and products. So for a good and healthy life of heavy smokers with these high-tech health products.

Find the perfect Airbnb for your next trip

StickyOscar

Selecting the top accommodation place is predominant for any kind of trips. Hotel rooms can be convenient and reliable, but booking Airbnb is cheaper, offers you more space for less money and is more fun to stay. With the Airbnb, you often get a better feel of living. You will get the best amenities at the Airbnb that you never get to other hotels. We all look for the most comfortable and luxury place, yet affordable. It applies when you choose the Airbnb for your next stay. If you are planning your next trip to Atlanta, then look for more information about the best Airbnb. It helps you to choose the best and reliable one without any hassles. Here are a few tips that you should keep in mind while choosing the Airbnb for your next trip.

Location:First of all, you have to decide on the perfect location to stay. You might have ideas for your trip and have to travel a lot for exploring many places in the city. So, choosing the location close to the city is essential. On the other hand, if you love to stay outside then search for the options. Keep in mind that nothing can ruin a vacation more quickly than being in the wrong location. If you are new to the place, then don’t worry Airbnb comes with the all essential details. It helps you to choose the most appropriate one for your needs. Make sure you end up choosing the preferred location.

Preferences in space:Next, you have the choice to choose the spaces in the accommodation with Airbnb. It is not possible with the hotels as you have only limited options. You should consider whether you need more living space or smaller. Depending on the number of people decide on a number of rooms you needed. You can also check for the other furniture, kitchen setup, themes and other features that you prefer.

List of amenities:After you decide the preferences, have a look at the list of amenities provided in the Airbnb. You can even check for the simple to necessary amenities. Also be sure to check the list of bed types, bathroom facilities and others. Make sure everything is listed before you book the apartment. Before you book Airbnb check for more information to make an informed decision. It will be more helpful for you to end up with the right accommodation with the right facilities. If you are travelling with your pets, then check whether pets are allowed.

Price:Another crucial factor that you have to consider and check is price transparency. You will get the Airbnb at the most affordable prices for you. Depending on the amenities and location the price might get varied. But it is always cheaper when compared to the hotels. Make sure that the price suits your budget. You can have a luxury living at reasonable prices. Hence, keep these points in mind while choosing the Airbnb for your next big trip.

The Financial Solutions For Every Company

StickyOscar

Almost all businesses today carry the target of gaining a profit and be successful in this industry. But to make it there, numerous battles will take over first to challenge every person who decided to enter this world. It’s a battleground, wherein only the strongest ones will remain. But even if the process may look hard, its successful results can greatly impact anyone’s life. It changed one’s life once everything went well and successfully in the business industry.

The way towards success in a company is a hard one. In gaining profit, the business should have a concrete plan to execute things and make things work in attaining its goal and vision in the future. If people develop strategies that are based on research, it will surely work together. Because surely, it will have a great impact on the overall state of the business.

Nowadays, many companies are struggling to gain profit. New businesses have a hard time establishing a great connection with their target, making it hard to gain profit. On the side of the established businesses, they have this pressure on how they will remain successful in the industry, especially now that the number of competitors increases. That’s why there is no doubt that many kinds of businesses nowadays face such financial crises and other types of challenges. These kinds of battles are normal or somehow inevitable to happen in this industry.

No matter how many challenges a business is facing, surely there are solutions to them. Now that society is facing its modernization, there are modern solutions to every challenge that any company may be facing now, as problems with finances.

The Status of the Businesses Today

In gaining profit, a good cash flow should exist in the company. It means great management of the overall movement of the finances coming in and out of business. Through this, its operations will continue to run smoothly. Because if not, it will just show a danger to the company.

Nowadays, one of the top reasons for the challenge in a good cash flow are the clients who are having unpaid transactions, and they are not paying on time. Once most of a company’s customers will be acting like this, the organization will soon get into the danger zone, wherein it will have a financial crisis.

There are many cases of slow-paying clients or customers nowadays. Because of the increased competition in the business industry, most of these companies let themselves offer such great opportunities and offers to their clients, giving a longer payment time. But this kind of strategy is sometimes dangerous, and now many companies are facing such difficulties to clear their invoices.

A Win-Win Modern Solution

There’s a modern solution to the problem with pending invoices through the help of florida factoring. They got the solution and best option for various companies’ needs on financial solutions. Their way of paying the pending unpaid invoices or transactions with their clients will help the company run the overall operations smoothly without compromising its image. It’s a great example of a win-win model solution now that every business should use.

Things You Might Want to Know About The Sahara Deserts

StickyOscar

Few other locations on Earth equate to the beautiful scenery that you can find in the Sahara Desert. Moving nearly north-south across Morocco’s eastern frontier with surrounding areas of Algeria, you can see the beautiful Sahara desert. It approximately has the scale of the United States as a whole. It is a fun fact why the Sahara Desert is the largest in the whole world. Many tourists visit Morocco primarily to delve further into the desert while enjoying an evening underneath the stars. A desert vacation is a memorable experience you’re not expected to miss out. With that said, here are some of the things that you might want to know before going on an adventure to the desert.

The temperature changes. You might want to check your weather tolerance. In the desert, the Sahara temperature varies depending on the time of the day. If you are there in the morning, you are most likely to experience the heat of maybe below 50 degrees celsius. If you convert that it will be 122 Fahrenheit. In many cases, people might not want this type of atmosphere. That is why make sure to put sunscreen on your skin. At night, the temperature actually goes down. It can go below at least 10 degrees celsius or 50 Fahrenheit. If you are planning to stay for the night, you can have stargazing and enjoy the breeze of the wind.

Consider the possibility of seeing snakes. One of the things that you might want to be aware of is the presence of snakes in the desert. That is why tour guides prepare themselves for these unlikely encounters. There are snakes in the desert that you might not know. It blends in beautifully with the sand which makes them not noticeable.

Trips to the Desert are doable. Of course, you can go on a trip to the Sahara Desert. There are camels that tour guides use as a means of transportation. It adds a little bit to the experience of traveling in the Desert. Moreover, you can even stay a day or two in the desert. You can also just go book accommodation if you want to visit the site in the morning only. There are websites online now that can help you with your itinerary regarding this matter. Make sure to visit them and see what they have in store for you.

Beautiful landscapes and rock formations. As a matter of fact, this is one of the reasons why people want to go to the Sahara Desert. People want to personally see the beautiful landscape of the sand. The landscapes of the sand formations are naturally created by the wind breeze as well as the emerging rocks or stones that naturally emerged in the desert. Moreover, during the night tourists can stay and enjoy a stargazing moment. You will have a full view of the sky. Making it even more magnificent to experience.

Knowing a little background of the place is a must have before you go on a trip. So be prepared and face the wondrous beauty that you can behold only in the Sahara Desert.

Installing a swimming pool isn’t as difficult as many think it is

StickyOscar

Have you been on the fence about having a swimming pool installed on your property? If so, you really shouldn’t be. Swimming pool installation is by far not as complicated as you think it is. A pool can be installed in your backyard quickly, and you can be swimming in no time. Suppose you have always desired to have the luxury of a swimming pool in your backyard, but you have been holding yourself back because of the false belief that installing a swimming pool is very complicated. In that case, you really need to rethink your point of view.

Installing a swimming pool is not as complicated as you may think it is

It doesn’t have to be a monumental problem. All you need is the right knowledge from the beginning, and a professional can install a pool in no time. The best part is, you don’t have to do anything at all. A team of professionals will come out and do all the work for you. You show them where to get started, and they’ll do the rest.

How to choose where to have your pool installed?

The most common choice is to have a pool installed in the backyard. Why? It’s because that’s where a home has the most space. It would seem a little odd to have a pool in your front yard. It’s too much water. And besides,, who wants to look at a swimming pool while you’re pulling into your driveway? It’s just not all that appealing.

You want to make sure that you are fully aware of your property lines when installing the pool.

Make sure that you know exactly where the edge of the pool will be and how it will look in relation to your house, driveway, and even any fences. More importantly, you don’t want your pool to end up on your neighbor’s property. This is crucial. If you don’t want your pool to end up in your neighbor’s back yard, then you’re going to have problems.

Before you decide to install a swimming pool, you will need to figure out how big a pool can fit your backyard.

This is very important. If you have a small backyard, you will need to make sure that the size of the pool fits. A pool that is too small will not look appealing. Too big, and your backyard won’t have enough space to properly fit in the pool. A professional can help you decide on the right size.

Remember, your backyard is a place to enjoy and relax

You don’t want the swimming pool to be the biggest thing in your backyard. Balance shouldn’t be a problem when installing a swimming pool in your backyard. The right size should give your backyard a nice look without overdoing it. Getting the right size pool will allow you to have a pool at home that will be as enjoyable as it is functional. You’ll use your pool quite a bit, and it will become the focal point of many fun-filled summer days.

What do You need To Know About Kitchen Cloud?

March 15, 2023 Oscar

A kitchen cloud, a virtual kitchen, ghost kitchen, or dark kitchen, is a restaurant concept that operates without a physical dining room or storefront. Instead, the focus is on food production and delivery, with orders placed online or through a mobile app.

Cloud kitchens typically operate out of large, centralized kitchens designed for efficiency and optimized for delivery. They may serve multiple restaurant brands, each with its unique menu, or they may focus on a single cuisine or food type.

The main advantage of a cloud kitchen is that it allows restaurant operators to reduce overhead costs by eliminating the need for a physical storefront or dining room. This can make it easier and more cost-effective to launch new restaurant concepts or expand existing ones. It can also enable restaurant operators to reach a wider audience by offering delivery and takeout options.

Cloud kitchens typically rely heavily on technology, with online ordering platforms, kitchen management systems, and delivery logistics software being key business model components. They also require a highly trained staff of chefs and kitchen workers who can quickly and efficiently produce high-quality food.

Overall, cloud kitchens are a relatively new concept rapidly gaining popularity in the restaurant industry, especially in urban areas where real estate costs are high and demand for delivery and takeout options is strong.

kitchen cloud

Following are the various benefits of cloud kitchens:

Lower Overhead Costs: Since cloud kitchens operate solely for food delivery purposes, there are no costs associated with physical restaurant spaces, such as rent, maintenance, utilities, or property taxes. As a result, cloud kitchens have lower overhead costs than traditional restaurants.

Flexibility: Cloud kitchens offer flexibility to their operators regarding the types of cuisines they can offer, the menus they can create, and the pricing structures they can implement. Additionally, cloud kitchens can be set up quickly and easily, allowing operators to test new concepts and menus without the risks and expenses of opening a traditional brick-and-mortar restaurant.

Increased Efficiency: Cloud kitchens are designed with efficiency in mind. With no need to manage a dining room, host guests, or manage servers, operators can focus solely on cooking and fulfilling orders, resulting in faster delivery times and more efficient operations.

Increased Reach: Cloud kitchens focus solely on delivery to reach a larger customer base than traditional brick-and-mortar restaurants. Operators can reach customers who may not have easy access to a physical restaurant location or prefer having food delivered directly to their doorstep.

Data-Driven Insights: Cloud kitchens rely heavily on technology, which provides operators with valuable data insights about their business, such as customer behavior and ordering patterns. This data can be used to optimize menus, pricing, and marketing strategies to serve customers better and increase revenue.

Cloud kitchens, virtual kitchens, work differently than traditional brick-and-mortar restaurants.

Kitchen Setup: The cloud kitchen is set up in a central location, often in an industrial area or a commercial kitchen facility. The kitchen has all the equipment, appliances, and utensils needed for cooking and preparing food.

Partnering with food delivery platforms: The cloud kitchen partners with food delivery platforms, such as GrubHub, DoorDash, Uber Eats, or Deliveroo, to receive customer orders.

Online Ordering: Customers place their orders through the food delivery platform’s website or mobile app, selecting the menu items they want to order and providing payment information.

Why is marketing important for home improvement contractors?

March 13, 2023 Oscar

In this marketing world, different fields use specific types of websites to attract the attention of larger customers over the internet. The way home contractors use to promote their business over the internet with new customers in their surrounding area. To attract more customers in the area, it is important to do marketing for home improvement contractors.

Most contractors use this internet marketing method, as it is one of the most popular ways to attract more customers by knowing their requirements. They help you with renovations and improve your home design based on individual personal preferences. The website will help to improve your overall impact on your home design.

Home improvement contractors provide maintenance, repairs, additions, and other required changes in your home. The marketing for home improvement contractors makes their service attractive and convincing enough to generate different changes to attract customers to choose your service. Home improvement contractors provide different services, including security systems, insulation services, wood renovation, fixing doors, and other services with different strategies.

The marketing service promotes your work on different services with time, price, quality of your service, and other services. The marketing service promotes making keywords related to your service available in different areas to different people looking for renovation and home improvement services. This method helps provide a different marketing plan for the development of your home improvement service. The target of this service is to promote your service and make it reach the top of search engine results.

When your service results at the top of the search, you will get more leads with different customers over the surrounding area. So, interested people can get your service by contacting you. It helps in the continuous growth of your industry.

By using this marketing method you can get

High paying clients
Target clients in a specific area
Create automated process
Get new clients without walking to their doorstep
And more

The marketing company promotes your business over the internet in the most effective ways

Web design
Search Engine Optimization
Content marketing
Pay-per-click Advertising
Email Marketing

These are the five common marketing tactics used by a marketing company to promote your business, but it is important to choose the right marketing company to increase your site traffic so you can place your service on the top page of the search results. It also plays a major role in building your company’s reputation in the online market and increasing your ranking over your competitors.

Looking For Wills And Trusts Attorneys In Billings, MT?

February 12, 2023 Oscar

Ritchie Manning Kautz PLLP is a reputable law firm based in Billings, MT, that provides legal services to clients in the surrounding area. Among their many areas of expertise, the firm is particularly well-known for their wills and trusts attorneys, who have been helping clients in Billings and beyond to secure their futures and protect their assets for many years. For those who are looking for wills and trusts attorneys in Billings, MT, the Ritchie Manning Kwills and Trusts team is the go-to choice. Their wills and trusts attorneys have the experience and knowledge necessary to help clients navigate the complex legal landscape surrounding estate planning and ensure that their wishes are accurately reflected in their legal documents. Whether a client seeks to create a simple will or establish a complex trust, the attorneys at Ritchie Manning Kautz PLLP have the skills and experience to provide effective guidance and representation.

They are multi-skilled

In addition to their experience in estate planning, the wills and trusts attorneys at Ritchie Manning Kautz PLLP are also well-versed in various related legal areas, including probate and estate administration, tax law, and elder law. This broad understanding of the legal landscape allows them to provide clients with a comprehensive view of their options and to offer tailored, effective solutions that meet their specific needs and goals.
The attorneys at Ritchie Manning Kautz PLLP are dedicated to providing their clients with the highest level of service and support. They take the time to listen to their client’s concerns, understand their goals, and provide straightforward, honest advice. Whether clients seek to protect their assets, ensure their wishes are carried out or navigate the probate process.

Concluding

For those who require reliable, effective legal wills and trust attorneys in Billings, MT, Ritchie Manning Kautz PLLP is a clear choice. With a team of skilled and experienced attorneys and a commitment to providing personalized, results-driven service, the firm has established itself as one of the leading wills and trusts law firms in the area. If you are looking to secure your future and protect your assets, the team at Ritchie Manning Kautz PLLP is here to help.

How to Prepare for Your Cosmetic Dentistry Procedure?

February 10, 2023 Oscar

Cosmetic dentistry is a field of dentistry that focuses on the aesthetic enhancement of your teeth and mouth. It involves a variety of procedures, such as teeth whitening, veneers, and dental implants. Each of these procedures requires special preparation, and it’s important to understand what needs to be done to ensure a successful result. We’ll discuss how to prepare for your cosmetic dentistry procedure.

Consult with Your Dentist:

The first step in preparing for your cosmetic dentistry procedure is to consult with your dentist. Your dentist will examine your teeth and gums and discuss the best options for you. They will also be able to explain the procedure in detail and answer any questions you may have.

Get a Comprehensive Exam:

Before undergoing a cosmetic dentistry procedure, it’s important to get a comprehensive exam. This exam will provide your dentist with detailed information about the condition of your teeth and gums. This will help them determine the most appropriate procedure for you.

Follow Pre-Procedure Instructions:

Once you’ve decided on the procedure you want to undergo, it’s important to follow all pre-procedure instructions given to you by your dentist. This can include dietary restrictions, avoiding certain medications, and abstaining from smoking or drinking.

Understand the Risks:

It’s important to understand the risks associated with your cosmetic dentistry procedure. Your dentist will be able to explain the potential risks and side effects, as well as how to minimize them. Your dentist should also explain the potential benefits of cosmetic dentistry and why they may recommend a particular procedure. You should also inquire about the cost of the procedure and if there are any financing options available.

Choose a Reputable Dentist:

When selecting a dentist for your cosmetic dentistry procedure, it’s important to choose one that’s reputable and experienced. Be sure to research the dentist’s qualifications and ask them any questions you may have.

Follow Post-Procedure Instructions:

Once your cosmetic dentistry procedure is complete, it’s important to follow all post-procedure instructions given to you by your dentist. It’s important to follow all instructions to ensure a successful outcome.

Schedule Follow-up Appointments:

Finally, it’s important to schedule follow-up appointments with your dentist. These appointments will allow your dentist to monitor the progress of your treatment and make any necessary adjustments. Regular follow-up appointments are essential for your oral health. They help detect any changes in your mouth and ensure that your treatment is working as it should. This can help prevent any future problems from arising and maintain the overall health of your teeth and gums.

Conclusion:

Preparing for a cosmetic dentistry procedure is important to ensure a successful outcome. Taking these steps will help you achieve the best possible results.

What you should know before buying a used car?

February 5, 2023 Oscar

Addressing while you are buying an item is an incredible method for expanding generally speaking mastery and information, especially when it’s a raised exchange like this. Pose the suitable inquiries, and the reactions you get may impact the decision in regards to the decision about whether to proceed with the obtaining of a recycled vehicle.

How old is by all accounts the vehicle truly? is the principal thing you really want to learn. It’s fundamental since you can resolve the deteriorated esteem and the right expense to be paid for the specific vehicle in the year that it was constructed.
When and just when you are getting an authorized vehicle from a decent and solid trade-in vehicle vendor like used cars in san diego, you should ask the merchant the explanation they will offer the engine (like Revv). Who knew, maybe the vehicle has a difficult issue and that is the explanation they’re attempting to advance it. The checks led prior to purchasing would uncover the state of the vehicle, hence the proprietor ought to have the option to sincerely answer to this inquiry.
What distance has the vehicle previously traveled, in miles? Learning about this issue is something that each pre-owned auto top pick would encourage anybody to do! Everybody is aware of how critical great gas mileage is. You should know about the specific mileage the vehicle has previously logged. Indeed, even this says something regarding a ultimate conclusion about the vehicle’s cost.
Is the vehicle covered by an insurance? An additional advantage while purchasing a pre-owned vehicle is a maker’s guarantee. On the off chance that you approach such a vehicle, don’t disregard it. It could make a phenomenal find at utilized vehicle costs.

At the point when you as of now have an insurance contract, make a point to possibly at any point confirm to check whether your new vehicle might supplant your old one. It is typically judicious to ask the proprietor on the off chance that the pre-owned auto you are buying has an ongoing strategy, however a security expert could advise against this. In such a circumstance, you might be compelled to collapse any one strategy.

See whether the vehicle is authorized on the off chance that you intend to buy it through a firm like Revv, which sells old vehicles, offers premium types of assistance, and rents out vehicles. This is an important point since confirmation which was before vehicles, that came profoundly fitting, are the best prospects to consider while purchasing a pre-owned vehicle.

How to Use a Home Security Safe?

January 15, 2023 Oscar

A home security safe is a great option for keeping valuable items safe and secure from theft, fire, and other damage. It is important to understand how to use a safe correctly to do this. This article will explain the steps to use a home security safe and the benefits of having one in the home.

Choose the Right Size:

The first step in using a home security safe is to choose the right size for your needs. You will want to make sure the safe is large enough to fit all of the items you want to keep inside and also small enough so that it can fit in the desired location.

Install the Safe:

Next, you will need to install the home security safe in the desired location. Depending on the type of safe you have, you may need to mount it to a wall or have it bolted to the floor. Make sure to follow the instructions provided with the safe to ensure proper installation.

Choose a Combination:

Once the safe is installed, you will need to choose a combination that you will remember. You will also want to make sure the combination is not easily guessed by others.

Set the Safety Features:

Your home security safe may come with additional safety features such as an alarm, biometric scanner, or other technologies. Make sure to set these up according to the instructions provided with the safe.

Store Your Items:

Now that the safe is installed and set up, you can begin to store your items inside. Make sure to organize the items you store in the safe to make them easier to find. You can also consider using labels or dividers to help you keep track of the items stored in the safe. You should also record the combination of the safe and store it in a secure location, such as a fireproof lockbox or safe deposit box.

Lock the Safe:

Once all of your items are stored inside the safe, you will need to lock the safe. Again, make sure to follow the instructions provided with the safe to ensure it is properly locked.

Test the Combination:

Once the safe is locked, you will want to make sure the combination works by testing it. Make sure to test the combination several times to make sure it is correct. If the combination does not work, you will need to contact the manufacturer or a locksmith to have the safe opened.

Monitor the Safe:

Lastly, it is important to monitor the safe and make sure it remains locked. You should also check the safe regularly to make sure it is still in good condition. It is also important to keep track of who has access to the safe and to keep a log of when it is opened and closed. This will help you to know who has access to the safe and when it is being used.

Conclusion:

Using a home security safe is a great way to keep valuable items safe and secure. By following these steps, you can make sure your items are properly secured and that you have access to them if needed. Make sure to monitor the safe regularly to ensure it is still in good condition.